高中数学教学研究：杨辉三角与二项式系数性质

1.HPM教学片段

本节知识将数学史料“杨辉三角”作为新课内容的讲解工具，所以教师务必深入研究教材，进行教材设计.以下为具体教学片段.

师：同学们，在上节课的学习过程中，我们知道了二项式定理为：

还学习了二项展开式中的各项系数叫作什么？

生：二项式系数.

师：值得注意的是，它们是一组仅与二项式次数n有关的n+1个组合数，与a,b没有关系，那么同学们想想，展开式的“二项式系数”和“系数”是一样的吗？为什么？

生：不一样，展开式中的系数与a,b的大小是有关系的.

师：很好，接下来就请同学们计算一下对于(a+b)n，当n=0,1,2,3,4,5,6时，展开式的二次项系数，填写教材32页的表格.

好，现在我们已经得到了()n

a+b的系数表，如图7-2所示.

图7-2　(a+bn)的系数表

同学们，这样的一个三角形的图形表，就叫作二项式系数表.那么你们能借助这个表来发现一些新的规律吗？

生：每一行的两边都是数字1！

师：对啦，那么同学们知道这是为什么吗？

生：因为二项式系数

师：好，我们继续横向来观察每一行的数，除了两头均为1，还有什么特点？

生：它的数是左右对称的.

师：那么转变为二项式系数的性质，是什么？

生：

师：这实际上就是我们学习的组合数的性质，是吧.而且我们再来看，每一行数的增减性如何？

生：从左往右看，是先增后减.

师：也就是中间的数是什么？

生：最大值.(www.xing528.com)

师：好，现在请同学们用数学语言准确地描述出来.

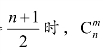生：当n为偶数时，对于二项式系数逐渐增大；当m≥逐渐减小.中间的二项式系数时，取得最大值.当n为奇数时，当m逐渐增大，当m≥逐渐减小.中间的二项式系数是相等的，同时取得最大值.

师：对了！要注意，当n为奇数时，中间的两个数都为最大值.同学们，那么现在我们就根据对每一行的横向观察得到了二项式系数的对称性、增减性和最大值了.接下来能不能试着纵向观察呢？又能得到什么性质？

生：表中除了左右两端的1，其他数都等于肩上两数相加的和！

师：非常正确！所以对于n＝7，n＝8时，同学们能不能直接写出它的二项式系数？用不用再去进行庞大的计算？

生：不用啦，n＝7时，它的二项式系数依次为1，7，21，35，35，21，7，1；n＝8时，依次就为1，8，28，56，70，56，28，8，1.

师：很神奇对吧？那么根据这个特点我们又能得到二项式系数的什么性质，大家想想.

生：

师：这也是我们之前学过的组合数的性质吧！现在同学们将二项式系数表跟图7-3的这个表比较一下，是一样的吗？

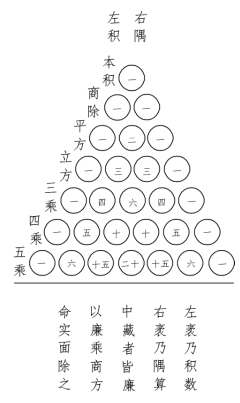
图7-3　杨辉三角

生：是，只不过阿拉伯数学变成了汉字.

师：是的，它们其实就是一个表.值得指出的是，这个表大约在公元11世纪的时候就被北宋数学家贾宪首创，并在《释索》算术中记录了！后来南宋数学家杨辉在《详解九章算法》中引用了此表，所以二项式系数表又称为贾宪三角或杨辉三角，它与欧洲的帕斯卡三角一致，但却比它先创了五百年！由此可见，我国古代数学家付出了多少汗水，他们的成就值得我们整个中华民族自豪！

也就是说，我们刚刚是通过杨辉三角直观地观察出这么多关于二项式系数的性质.所以古代数学的成就，其功能和奥秘是值得我们不断探索和挖掘的.

那么除了这个方法，我们也可以从函数的角度去探究性质，即将看成以x为自变量的离散函数f(x).下面我们一起来看.

2.教学分析

下面我将从教学过程和教学现状两个方面来进行教学分析.

以上教学片段依照教材内容，先引导学生根据已学过的知识列出二项式系数表，再借助此表去发现有关二项式系数的一系列性质：

（1）每行两端都是1：

（2）与两端的1等距离的数相等，即对称性：

（3）增减性与最大值：当n为偶数时，最大；当n为奇数时，最大.

（4）在相邻的两行中，除“1”以外的每一个数都等于它“肩上”两个数的和：

最后再与古代数学家的成就“杨辉三角”对比，发现是一致的，由此对我国古代数学的成就“杨辉三角”进行介绍，以便向同学们展示它的魅力.

在实际课堂教学中，部分教师会按照教材中的编排方式，先找规律引出性质，再指出“杨辉三角”这个伟大的古代数学成就，也有部分教师会先介绍“杨辉三角”，再找规律.但总的来说，他们都是通过“杨辉三角”这个形式来探究发现二项式系数的性质，并着重突出我国古代数学的成就，与教材内容一致.这样的教学会让学生体会到我国古代的数学成就是巨大的，从而触发其爱国情感和身处新时代的使命感.