教师认知概率知识：实践取向研究

1.教师对“概率”知识的认知调查分析

为了了解教师对“概率”知识的认知情况，在问卷中共设计了十道题，分别是第1,2,3,4,5,6,9,11,16,21题.

第2题主要是了解教师对“概率”知识地位的认识状况，进而了解其对课标的把握情况.调查情况如表6-3所示.

表6-3　“概率”知识地位认知

从表6-3中的数据结果分析得出：认可“概率”基础知识已经成为一个未来公民必备常识这一观念的教师所占比例为95.2%，无反对者，说明在教师群体中这一观念基本上已经成为一种共识.我们身处在一个瞬息万变的信息时代，如何在纷繁的数据中捕捉有价值的信息并以此做出合理决策已经成为每个公民的必备能力.然而数据信息的处理必然离不开随机思想及概率基础知识，故而其作为公民常识性知识的普及已成为一种必然.整个数学课程改革的基调之一就是“培养未来公民的数学素养”，概率恰好充分体现了这一点.从数据可以看出，绝大部分教师对“概率”内容在整个数学课程中的地位、教育价值有着较为清晰的认识，同时也只有准确把握这些，教学时才能做到心中有数，才能有意识地向它靠拢.但是依然存在部分教师持不置可否态度，分析其原因为：首先，部分教师缺乏对课程标准的深入解读，以致对概率的定位及要求认识模糊；其次，思想上没有引起足够的重视，只是为了考试而教学，只关注知识本身以及对学生的评价标准，陷入了“教教材”的小圈子里，不能从全局上对其定位进行把握，造成对其不甚了解的情况，在这种观念支配下的教学往往会与课标提出的数学素养教学相去甚远.

第1,4题主要是了解教师对概率与日常学习和生活联系的认识情况，其数据统计情况如表6-4所示.

表6-4　“概率”与日常学习生活联系认识

第1题主要是调查教师对生活中概率的认识情况.由表6-4中数据可知，所有被试者均认为概率与我们的日常生活息息相关，在这一点上认识比较一致，这也是教师对生活的一个直观体验.数学家拉普拉斯说：“生活中最重要的问题，其中绝大多数在实质上只是概率问题.”概率论是“生活真正的领路人，如果没有对概率的某种估计，我们将寸步难移，无所作为.”上面的论断看起来比较夸张，但也从侧面说明了概率与现实生活的联系比较紧密，同时我们也能时刻感受到概率思想、随机现象在日常生活中的普遍存在性.如校运动会抽签决定比赛对手，篮球比赛的投篮命中率，明天持续高温的可能性，股票涨跌预测，风险投资评估，等等.

第4题主要是调查在学习工作中对概率思想的运用情况.由表6-4中数据的分布情况可以初步了解，约66.7%的老师比较赞成在学习工作中较多地运用或接触到概率思想这一观点，但存在部分教师持不赞同或不置可否态度.为了进一步探究各因素对其影响情况，针对第4题的态度选择情况与各因素间是否存在显著性差异进行卡方检验，其数据如表6-5所示.

表6-5　概率思想在学习工作中运用情况认知差异的影响因素

由表6-5中数据可以发现，教龄、学历以及参加教师培训次数的不同在第4题上的选择情况上不存在显著性差异（p＞0.05）.这说明虽然教龄、学历、参加教师培训次数等因素不同，但并不影响对它的选择，大家在学习工作中对概率及概率思想的运用情况差别不大.

第3,11题主要是调查课改后教师对“概率”内容高考考查要求的认识情况.其统计数据如表6-6所示.

表6-6　高考概率要求的认识

由表6-6中数据可以清晰地看出，在第3题的调查中约69.8%的教师认同课改后概率的考查方向及比重不会产生大的变动这一观点.首先从课时设计上看，《大纲》版在必修概率部分有12课时，选修Ⅱ中统计与概率合计14课时，累计26课时，而《标准》版在必修3中关于概率章节有8课时，选修2-3中统计与概率22课时，合计有30课时，故而从课时的总量对比上可以粗略看出关于概率板块的考查比重不会发生太大变化.其次认真对比《大纲》版和《标准》版教材关于概率内容的设计及教学目标不难发现对概率要求的变化.总体而言，对概率的考查方向不会发生太大的变动，但局部侧重点发生了变化，比如关于互斥事件，《大纲》版教材给出的教学目标是了解互斥事件的意义，会用互斥事件的概率加法公式计算一些事件的概率，而《标准》版教材则是通过实例了解两个互斥事件的概率加法公式；《大纲》版教材的落脚点在于“会用”“会计算”，而《标准》版教材的落脚点在于“了解”.另外，在选修部分将重点放在了超几何分布与二项式分布上.关于这种变动相对较多，这里就不一一赘述了.2013年四川省迎来了课改后的首届高考，对比分析这两年的概率解答题也可以印证上面的观点.另外，约占30.2%的教师持不置可否和不赞成的态度.造成这一认识的原因有以下两点：一是对课改前后教材内容及要求的对比不够清晰；二是新增内容诸如几何概型、超几何分布、条件概率等相关新增知识点影响对其整体的把握.

由11题的统计数据可以看出，大部分教师认为，高考对概率的考查重点依然会放在如何计数上，另一部分教师持不置可否态度，只有小部分教师持不赞成态度.为此，针对此问题进一步访谈了某中学高二年级数学老师：（注：A代表访谈者、B代表被访谈者）

A：大部分教师认为，高考对概率的考查重点依然会放在如何计数上，您怎么看？

B：随机观念、随机意识在高考试卷中难以以具体形式呈现，所以高考考查应该落脚于对概念、定理、模型本质的认识和理解上，最终体现在概率解题中，而“计数”作为一个重要环节，无法忽视.

因此，结合访谈及对比教材及其说明可以看出，以往注重计算而《标准》版教材淡化计算，把培养随机观念放在了首位.由此可见，大部分教师还没有跳出以往的“圈子”，观念的转变尚不到位，其中最主要原因是高中教师不得不面对的高考问题，一切以成绩论成败，功利思想比较普遍，概率教学的重点是随机性思想的培养，但这却难以量化，无法进行有效的考查，进而在一定程度上被概率的解题、计数所取代，这也是多年根深蒂固的应试教育思想所造成的.综观如今的考核可以发现，考核注重考查学生对数学概念、定理等本质的理解，注重考试内容进一步贴近时代、贴近社会、贴近考生实际，注重考查考生运用所学知识分析问题、解决问题的能力，控制单纯、烦琐的运算，体现了“多想少算”的命题理念.因此，要准确地把握高考对概率的考查方向及侧重点，需要认真研读课程标准解读.

第5,16题主要是了解教师对概率与统计的联系的认识情况.其统计数据如表6-7所示.

表6-7　概率与统计联系的认知

从第5,16题的回答情况可以看出，绝大部分教师认同在利用随机思想解决问题的过程中将大量用到统计的思想与方法以及在统计与决策的过程中蕴含随机思想这一观点.另有部分教师持不置可否、不赞成态度的分别约占14.3%，4.8%；6.4%，11.1%，造成这一现象的原因是部分教师对概率与统计间的联系理解得不够深刻或者把概率与统计视为相对独立的两个板块，对它们之间的关联没有做深入思考.概率定义充分说明了概率与统计之间的联系——“在相同的条件S下重复n次试验，观察某一事件A是否出现，称n次试验中事件A出现的次数nA为事件A出现的频数，事件A出现的比例为事件A出现的频率，事件A发生的频率fn(A)随着试验次数的增加稳定于概率P(A)，因此可以用频率fn(A)来估计概率P(A)”.因为这个定义是通过统计观察计数分析而抽象出来的，所以我们把这一概率定义称为概率的统计定义.但16题中不赞成所占比例相对略大，为了探究影响16题认知差异的主导因素，下面对第16题的回答情况与各因素间的关系做卡方分析，统计结果如表6-8所示.

表6-8　概率与统计联系认知差异的影响因素

由表6-8中的数据可知，教龄增长、学历提高以及参加教师培训次数的不同在第16题上的选择情况上不存在显著性差异（p＞0.05），由此说明，教师对统计与概率联系的认识相对而言比较一致.(www.xing528.com)

第6，9题的设置主要是了解教师对古典概型与几何概型联系的认识情况，21题主要是通过教师侧面了解学生对它的认知情况.其统计数据如表6-9，6-10所示.

表6-9　古典概型与几何概型联系认知

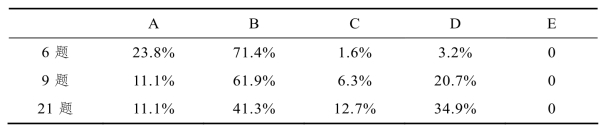
表6-10　古典概型与几何概型联系认知的影响因素

从第6题的调查结果看，绝大部分教师认同事件的等可能性既是古典概型运用的基础也是几何概型的条件这一观点，只有极少数部分教师持不置可否及反对态度.从卡方检验结果来看，教龄（p＜0.05）以及学历（p＜0.01）两个因素在古典概型和几何概型联系的认识上具有显著性差异，特别是在学历这个因素上对其影响极其显著，故而说明一线教师在两种概型的联系认识上总体而言都比较到位.随着教龄的增加以及中学教师队伍整体学历的提高，对这两种概型联系的认识变得更加深刻.

第9题主要是调查教师对古典概型与几何概型主要区别的认识情况.从表6-9中数据可以看出，11.1%的教师非常赞同其主要区别是试验结果“是否”为有限个，61.9%的教师持赞同态度，几何概型是另一类等可能概型，它与古典概型的区别在于试验的结果为无限个；另有约占 6.3%的教师持不置可否和20.7%的教师持不赞同态度.由此可以看出，还存在相当一部分教师在这两种概型区别的认识上比较模糊或错误，这也进一步突显了概型教学的重点和难点之处.因几何概型与生活比较贴近，通过对几何概型的了解就可以更好地解释生活中的一些常见事件，故而课改后在概率板块新增了此内容；虽然几何概型在大学的《数理统计》中学过，但对于部分一线教师而言，时隔多年，出现一定的遗忘，加之对两种概型的定义对比理解不深刻，似是而非，所以才造成了以上近30%的教师持不置可否或不赞成态度.再结合卡方检验数据看，说明年龄、教龄、学历及参加教师培训次数（p＞0.05）的差异对其影响不大，这进一步说明教师培训在新增知识点的培训方面存在不足之处，教师培训往往从宏观上对课改后高中数学体系、要求做一些必要的讲解，但较少针对变动较大的版块，教师难教学生难学之处开展专题讲解，所以往后的教师培训可以根据教师的诉求进行一些有针对性的专题讲解.教师也应该不断“充电”，以提高自身的数学专业素养来应对不断变化的教育形式和改革.

为了进一步了解教师对概率“知识”方面的认知，对某中学部分年轻教师进行了访谈，此处列举两种认知错误或模糊的典型回答：

A：您对“概率为0的事件就是不可能事件”及“概率就是频率的极限或近似值”这两个问题是如何看的？请举例说明.

B1：概率为0的事件就是不可能事件，比如太阳从西边升起的概率为0，它是不可能事件；我们在实际应用中经常把频率的近似值看成其概率，同时在试验次数极大时，频率是逼近概率的，故而从这个角度来说“概率就是频率的极限或近似值”没问题.

B2：我们说“不可能事件的概率为0”但却没有“概率为0的事件就是不可能事件”这一说法，但举例比较困难，暂时找不到合适的例子；同样的“概率就是频率的极限或近似值”这一说法很少见，感觉存在问题但却说不出它具体错在哪里，有点模糊.

针对上面访谈中两种典型的回答可以明显看出，部分年轻教师在概率某些“知识”层面的认知还存在问题.在原有教材中教师一般会在教学中强调“概率为0的事件就是不可能事件”这一论断是错误的，但却很少举例说明，学生也仅仅是记住了“结论”，没有真正理解其中的错误点，但《标准》版教材引入了几何概型，从几何概型的角度列举反例就易如反掌.同时从访谈中可以看出，对“概率就是频率的极限或近似值”这一问题的看法存在极大的问题，我们在应用中一般“习惯”把“频率”近似地看成“概率”，并以此认为“频率是概率的近似值”，这显然是一种误读.同样地，我们把事件发生的频率随着试验次数的增加稳定于概率的认知误解为“概率是频率的极限”，概率的统计定义只是在描述上类似于极限的定义，但其与数学分析中的极限定义是有严格区别的，这里的“稳定”就是我们理解的“逐渐靠近”.但这仅是直观上的描述，其数学意义在《概率论与数理统计教程》中由伯努利大数定理（设nμ是n重伯努利试验中事件A出现的次数，又A在每次试验中出现的概率为p(0＜p＜1)，则对任意的ε，有以其严格的数学形式精确地揭示了频率与概率的关系，即频率依概率“收敛”于概率p.

第21题主要是从教师角度调查在教学过程中，学生在对古典概型及几何概型在这个问题上的选择比较分散，持赞同和不赞同或不置可否的比例几乎各占50%.为进一步了解造成其上选择情况的原因，进行了如下访谈：

A：在“学生在区分几何概型与古典概型时非常困难”这一观点的认识上，赞同和不赞同几乎各占一半，您如何看这种情况？

B：在这个问题上不能一刀切，影响学生区分的因素很多，存在教师对知识点的把握剖析情况、生源质量、知识点本身特点等诸多因素.

结合调查统计及访谈可以看出出现这种现象的原因如下：

（1）参加培训的教师来自各个区县的不同学校，从第6,9题的统计数据可以看出，存在相当一部分的教师对概型的联系与区别的认识上存在问题，故而在教学中就难以进行透彻的分析与讲解，进而影响学生对它的认识.

（2）学生结构的差异性（地域差异、班级层次差异、生源质量差异）造成认知情况的差异.

（3）教师的引导方式、教学方式方法不尽相同，情况复杂，所以学生在区分几何概型和古典概型时所遇困难也就不同.

（4）概型自身的特点决定了区别的难度.古典概型及几何概型的主要区别在于试验结果的有限与无限，从有限到无限的过渡本身就是一个难点所在.

从卡方检验数据看，年龄、教龄、学历及参加教师培训次数（p＞0.05）的不同对学生在这两种概型的区分难易程度上不存在显著性差异.

2.反思

通过对“概率”知识的认知问卷调查与访谈可以初步了解一线教师对概率知识的认知情况，由此产生以下两点关于知识定位及知识储备的反思：

（1）教师对概率知识的理解是否透彻、认识是否清晰，对概率知识的定位是否准确.

课改后与概率内容相关的知识做了相应的调整，也增加了部分新内容，对概率的要求、培养侧重点、考查等也做了一些微调.本部分内容的课时比例与高考考查比例的不协调无形之中也增加了教师的疑惑.新增内容有几何概型、随机数、随机模拟、条件概型、超几何分布等，这些新增内容对一线教师而言相对陌生，因为这些内容以前在高中没有接触过，都是在大学阶段才有所了解，但大学的学习是粗线条的，并没有进行深入透彻的研究，时隔多年几乎遗忘但却要成为高中教学的一部分，致使很多教师对这些新增知识点的认识存在偏差.另外，存在部分教师对知识点间的联系缺乏深入的思考，加之一些顽固的错误经验意识（如一对夫妻计划生2个孩子，这2个孩子是一男一女或全是男孩的概率不一样的错误认识），造成了对概率知识认识不透彻、不准确的现象.又如，在原有教材中理解“概率为1的事件为必然事件，概率为0的事件为不可能事件”相对比较吃力，但《标准》版教材中的几何概型却能够为其正确认识、理解提供简洁便利的实例.

另外，现在一线教师往往陷入这样一种“怪圈”，虽然课程改革后，教材以及考查方向都发生了部分变动，但教师并没有跟随课改的步伐不断更新自己的知识认知及定位，缺乏对教材及课程标准解读的足够重视，没有深入研读课程标准，加之应试功利思想的泛滥，故而造成了对概率知识的认识定位不准确.

（2）教师自身的知识储备及文化素养是否已经“到位”.

教师的素养达不到要求是影响课程改革效果的根本原因.学高为师，作为教师一定要不断充实自己使自身的知识储备达到一个高度，使知识更新处于一个动态的过程，也只有这样才能多角度、多层次的认识、全方位的理解教材知识点，也只有这样才能在课题引入时做到信手拈来，肢解知识点时做到举重若轻，课堂讲解时做到深入浅出.但由于部分教师知识储备不足，在概率知识点的认识上存在一些偏差与错误，比如古典概型与几何概型区别的认知，把概率理解为频率的极限，概率为1的事件为必然事件，两个事件并的概率如果等于两个事件的概率的和则认为这两个事件为互斥事件等错误理解.试想如果教师不能对概率知识点有着非常透彻的理解，又怎能搞好概率教学？学生又如何深刻理解知识点？