立体几何与空间向量-高中数学教学研究

空间向量本身具有代数与几何双重身份，它的出现可以将立体几何中基本元素间的位置关系转化为数量关系，能够让需要推理证明的结论用数量运算来取代.它从不同的角度去诠释立体几何，又以自身的独特性、优越性打破了公理化体系的瓶颈，使得让大众望而生畏的综合几何坠入“凡尘”，为更多的人所接纳.向量几何成为国际数学教育的一大特点.吴文俊先生根据现代化机械化的思想，认为：“对于几何，对于研究空间形式，你要真正的腾飞，不通过数量关系，我想不出有什么办法，当然欧几里得几何漂亮的定理有的是，漂亮的证明有的是，可是就算你陷在里面，你也跑不了多远……”空间向量的引入给立体几何注入了新鲜血液，体现了“通法”在立体几何解题中的优势.

当教师们正在为旧教材中引入空间向量，以数释形，用数量关系表达几何位置关系而解决“立体几何难学”这一问题而津津乐道时，文科立体几何又再次删除了空间向量要求.于此，文科立体几何的教与学似乎又面临新的挑战.

表5-14　教师对空间向量解立体几何工具性的认同分析

通过第13题的回答得知，几乎所有教师都认同空间向量在解立体几何问题中所体现的工具性作用，这无疑为文科生学习立体几何增添了乐趣，增强了信心（见表5-14）.在新教材中，突出运用综合法处理立体几何问题以培养学生的空间想象能力和逻辑推理能力，必修2中的一些重要定理，则是在选修2-1中用向量的方法加以证明的.虽然文科对选修2不做要求，但从教材整体的编排无疑再次说明空间向量在立体几何中的工具作用，向量法在一定程度上能够使立体几何问题得以简化，对解决立体几何问题有着十分重要的作用.

而在前面的论述中我们也提到，着眼于高考，文科立体几何的逻辑推理要求、考查力度（题目难度）是有所降低的.从教材的建构意图上来讲，新教材更加突出立体几何所带来的空间思维能力的训练，因此并不需要空间向量作支撑.至此，关于文科立体几何中的空间向量产生了截然不同的观点.

表5-15　教师对文科空间向量删除的认同分析

表5-15中的数据显示，空间向量对文科生是必要或不必要的几乎各占一半.这里虽然没有出现教龄对此的显著影响即老教师在教学中受惯性思维的影响，按部就班，但从统计图5-4中可以看到，对此持绝对反对意见的更多的还是那些教龄较长的老教师.

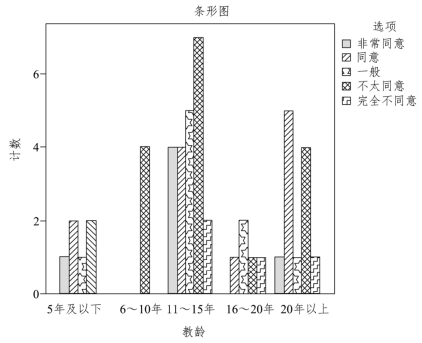
图5-4　教师教龄对空间向量删除的认同影响

在他们看来，现代科技引导立体几何发展趋于代数化，空间向量的出现可以将立体几何问题编译成计算机语言，使立体几何问题处理变得简洁高效，在这种情况下，让学生学习空间向量首先是符合时代背景的.而在实际教学中，空间向量为学生提供新的解题思路，学生可以根据实际问题、自身情况选择相应的方式解题.加之空间向量让立体几何程序化，文科学生通过理解加记忆的方式可以很快、很好地掌握，以降低立体几何的学习难度，增强学习信心，这也对学生数学学习兴趣的保持与提高有积极作用.(www.xing528.com)

也有老师强调，根据以往的调查，相比综合法，学生使用向量法的平均得分可提高5分左右.这在任何考试中都能拉开相当大的差距，那么在高考考场上，学生会用空间向量就显得尤为重要.文科立体几何在难度上，从整体来讲有所降低，但是二面角、线面角的计算仍然需要掌握，而文科生恰恰在准确找出平面角这个环节中有很大困难.有人说2021年各高考试卷鲜有计算线面角或二面角的考题，但这并不代表今后就只注重线面、面面位置关系或距离关系的考查.因此，空间向量可以成为文科学生解立体几何的最佳保障.

表5-16　教师对实际教学中补充空间向量的认知分析

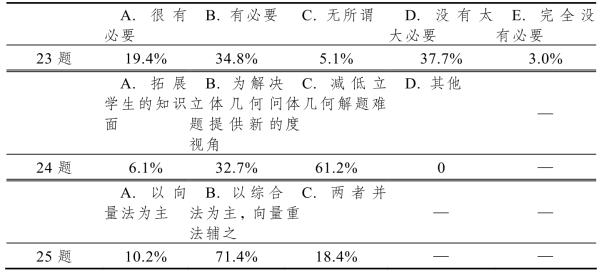
那么您认为有必要给文科学生补充空间向量吗？通过该问题的回答，同样印证了上面的结果（见表5-16）.不同的教师对于是否该为文科学生补充空间向量存在不同的看法，因为就空间向量对文科生后续学习的影响是有不同的认知的.有老师表示，删除空间向量是符合文科学生的发展要求的.不可否认，空间向量对学生眼界的开阔、接受新的事物都是有帮助的，但就未来择业而言，空间向量对文科学生所涉行业领域的影响是微乎其微的.因此，在高考指挥棒作用下，可以看到，对文科学生，立体几何的考查难度并不大，所有问题，即使没有空间向量，解决起来也不会很难；如果硬要补充的话，可能会加重学生的学习负担，同时空间向量的使用也会对学生产生误导.比如，对线面角的求解，法向量是与平面垂直的向量，它与已知向量所成的角并不是所求角，而是所求角的余角，不注意的话，学生非常容易出错.他特别提到，如果遇到的是一个斜棱柱之类的几何体，是不便于建立直角坐标系的，那么要用向量法去解题也是不科学的，因此，教学需要针对性.按最现实的意义来说，教学是要服务于高考的，因材施教才能实现收获的最大值.对于一个整体基础都很好，学习能力、接收能力都较强的班级，其实是可以适当补充空间向量的，这样更能保证他们在各种测试中都万无一失，但一定要强调向量法与综合法各自的适用范围，使学生能够在解题时判断哪种方法更简洁；如果教学对象的基础不够，补充空间向量不仅没多大帮助，反而还会加重他们的负担.新教材的编排已经在减轻学生负担，我们为何又要给他们加上呢？

立体几何的识图认图、点线面各元素间的位置关系、度量关系，在理解了性质、定理的基础上能够推理论证出其他命题等一系列教学要求，着实会给学生带来不小的压力.这既需要学生具有较强的空间想象能力，同时又必须有较好的抽象思维能力.而更多的老师为了降低立体几何的抽象性而主张向学生补充空间向量，这开阔了学生的眼界，为解立体几何题提供了新的视角.有老师认为，既然空间向量解题有很好的效果，为什么不能让学生有所了解呢？空间向量只是在平面向量的基础上增加了一个维度，那么通过平面向量进行类比教学，学生是容易接受的.一旦掌握了该方法，学生在遇到困难时，就可以选择这种解决方法，而不至于丢分.学习空间向量之后，学生也可以透过x,y,z轴确立的三个方向加深对空间几何体的认识.通过对“如果补充了空间向量，后续的教学您将如何进行”一问的回答情况来看（见表5-17），71.4%的教师都表示会以综合法为主，向量法辅之.其实这也从一个侧面说明，教师不会因为引入向量法而沉溺其中，他们表示，在教学中会强调综合法与向量法分别的优势与不足，并让学生学会区分在何种情况下选择何种方法解题.

表5-17　教师对补充空间向量影响分析

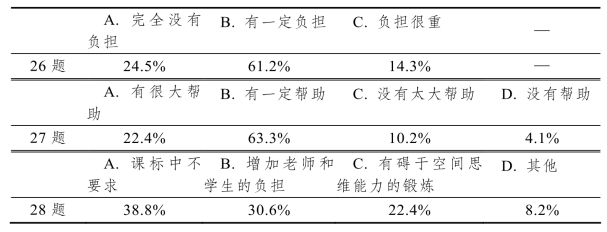
但我们必须面对一个现实问题：我们的教学进度如何保证？不可否认，额外补充知识，这样会对教师的教学产生一定的影响.其中 14.3%的老师认为这样做会有较大的教学压力，毕竟每节内容都有相应的课时安排.但85%以上的教师认为空间向量确实在降低学生学习压力的同时，也为教师的后续教学有很大帮助.

有教师以南充一中教学安排为例，认为各学校教学安排的灵活性是很大的，学校的课时量很充足，高二文科至少可以提前一个月的时间完成期末考核所有内容，这段时间由教师自行安排复习内容，丝毫不会影响课程进度.而此时理科还要专门进行空间向量的学习，所以文科教学可以紧跟理科的节奏，为学生补充一定空间向量的知识.因此，在很多老师看来，这是为文科学生补充空间向量的绝好时机.虽然各学校的实际情况不太一致，但这或许也存在一定的借鉴价值.

有老师坦言，往大里说，补充空间向量是违背了新课标的要求，虽然我们的希望是让学生通过学习达到能力的提升，但现实的评价标准依然是分数.空间向量能很好地满足“抓分”这一需求，这也在很大程度上减少了学生的心理负担，降低他们对数学的畏惧感.新教材对文科生不要求掌握空间向量，那么立体几何考题的设置也会有相应的导向，甚至有的考题会为向量法故意制造障碍，不便建系或不便计算，向量法虽是解立体几何的通法，但并不是所有题目都适合使用.所以，我们可以把它看成一个辅助工具，也应让学生明确它的价值所在.在综合法与向量法中各取所长，在不同的问题中选择恰当的应对方法，这是我们需要教给学生的.

综上所述，文科立体几何引入空间向量似乎已经找到极为可靠的支撑，一切困扰也尽在一线教师的掌控之中，也为众多文科数学教师认可接纳，但不得不说的是，所有的这些理由均是被应试教育指导模式所合理化的，所有“论据”也都是在极大地附和考试要求与“分数”评价体系.文理分科是为了符合社会发展的不同需求，不同的个体在社会中都有各自的价值体现，而教材内容就是专门为实现不同发展需求而精心制定的.从本质上讲，一线教师为学生补充空间向量与其说是为了扩大视野，降低立体几何的学习难度，不如说是为各种考试添加保险系数.应试教育的理念深入人心，因此教师们担心学生没有空间向量这一工具会在立体几何学习中遇到很大的困难，但这是不是有杞人忧天的意味在里面呢？当然，在学生问卷中，学生们也明确表示了对空间向量的“好感”，但从测试卷的结果来看，学生对综合法的掌握与应用情况远比我们想像得好很多，学生的这一能力是需要教师给予肯定的.线面角、二面角的求解确实是让很多学生头疼的问题，那为何不把补充空间向量所花的时间用于线面角、二面角的巩固加深呢？其中，帮助学生解决二面角问题也是教师“赋予”空间向量最强大的功能，因为它直接避开了对空间想象能力的要求，而找二面角的过程又是拓展学生空间思维能力的最佳训练途径.对引入空间向量这一问题存有争议，其中一个重要原因就在于它对空间想象能力要求的削弱，这一点也是与立体几何的教学功能背道而驰的.因此，以谋取分数为目的牺牲锻炼空间思维能力的机会是有失妥当的.