立体几何除了发展学生的空间思维能力和想象能力外,对于发展学生的论证推理能力、合情推理能力也会有极大的促进作用,能进一步锻炼学生的逻辑思维.当我们认识线面、面面平行和垂直时,新教材对其性质、定理运用公理化的方法进行了严格的推理说明;而判定定理的给出则充分体现了“直观感知、操作确认”,让学生通过观察、思考,合理使用手中模具,恰当利用合情推理,以对判定定理进行确认,再利用选修2-1中的空间向量来完善其证明过程.纵观整个教材编排,除了体现公理化方法的严谨性,也运用了合情推理方式的有效性,为学生思考问题、解决问题提供了新的视角;其独立出来的空间向量与立体几何部分,不仅凸显了空间向量在解决立体几何问题中的工具作用,还对合情推理结论的不严密做了补充,使得整个立体几何部分形成了一个严密的逻辑体系.
表5-12 教师对立体几何逻辑推理要求的认知分析

为了了解教师对新教材中逻辑推理内容的认知与实践操作,我们设置了相关问题(见表5-12).在谈及应加强文科学生的“空间认知,操作确认”时,教师对此有较高的认同度,几乎占调查总数的90%.高中文科学生抽象思维水平较低,但形象思维、直觉思维品质较好;在数学学习中,对于具体事物、直观图形的认识及文字语言之间的转化能力等表现较好.他们愿意动手做一些实物模型,易于接受直观简洁的描述,但对数学语言与符号语言的转化,以及对其进行的推理论证接受起来较为困难.结合他们这一思维特点,在以“空间几何体”“三视图和直观图”积累丰富表象后,加之动手操作,一些抽象的推理说明也会变得显而易见.苏联教育心理学家克鲁捷茨基认为“学生在学习数学的能力上有差异,但他们也具有各自不同的潜能,教师的任务就是帮助学生去挖掘这种潜能,使每个学生的全部能力都得到最大限度的发展.”
正因如此,接近八成的老师认为这是文科立体几何逻辑推理要求有所降低的信号.结合各市区的调研、模拟试题以及2020年各省市(包括四川省)的高考题,相较于以前的文科立体几何测试题,逻辑论证的难度有所降低,大多数省市均是将第一小问作为逻辑推理能力的考查,并集中在线面平行关系和线面垂直关系的证明上.处理线面平行,不外乎以线线平行和面面平行为踏板.纵观2020年考题,可以说运用面面平行“一招”便可“制胜”.高中立体几何课程历来以培养逻辑思维能力为主要目的,而新课标更加强调空间想象能力的培养,强调空间观念的建立,而逻辑思维能力的培养退至次要地位.
值得注意的是,还有超过20%的老师因为缺少空间向量而认为纯综合几何会给文科学生带来更大的挑战;加之三垂线定理及其逆定理的删除,原本能够通过定理直接得出的结论需要学生自行证明;一道线面垂直或线线垂直的题目,原本简单几步便能解决,现在却需多次利用线面垂直方可解决,为学生解题带来了一定的困扰.当然,教师之中对此也存在截然不同的看法,认为三垂线定理及其逆定理的删除,必定会降低作角、找角的要求,线面角、二面角的求解难度必定会下降.因此,教师对新教材删除相关定理的做法出现较大分歧,20.4%的教师认为合理,46.9%的教师认为不合理.
然而新课标所要求的,判定定理只要求直观感知、操作确认,而在选修2中加以论证.选修2是理科学生的学习内容,那么没有了空间向量对判定定理的证明,对于文科立体几何不就缺乏完整的逻辑结构吗?缺少严格证明,这势必会让学生产生困惑:“这样的结论可靠吗?”作为教师,要不要向学生进行严格证明呢?在实际教学中,教师又是如何处理这一问题的呢?
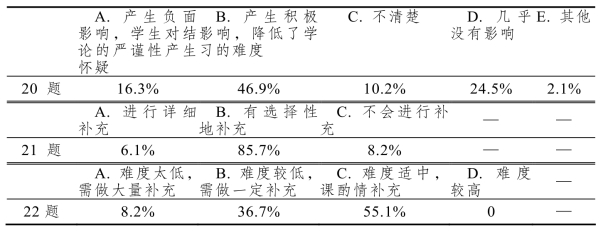
表5-13 教师对省略判定定理证明过程的认知与操作分析
 (https://www.xing528.com)
(https://www.xing528.com)
如表5-13所示,通过第20题的调查结果发现,更多的老师认为,判定定理不做证明,对学生是有积极影响的,这在后面的访谈中也再次得到一些老师的肯定;判定定理不做证明,会降低文科学生的学习难度,并不会对学生产生负面影响.加之,判定定理的证明更多使用的是反证法,这并不符合四川高考的考查模式,基本不会出现对判定定理证明的考查.对文科学生而言,判定定理是他们的解题武器,重点在于如何运用,不用深究其根源,否则,反倒会让学生抓不住重点,整堂课形散神也散.这也使得更多教师更倾向于在例题部分做扩充.
但在教学过程中,接近90%的老师会对判定定理的证明过程进行选择性的补充(由21题结果显示).其实,深入研究教材也会发现,这里省略判定定理的证明过程多少有些无奈.我们知道,判定定理的证明,借助平面向量是比较恰当的,但按照教材“1,2,3,4,5”的编写顺序,平面向量的学习是在立体几何之后的,所以此证明过程不宜给出.但在“1,4,5,2,3”教材使用顺序下,立体几何是在平面向量之后学习的,那么此时补充其证明过程是可行的,也不会给学生带来过多的压力.
在访谈中,钟老师给出一个较为可取的做法,她专门突出了“选择性”三个字,这里尤其是对教学对象的“选择”.对于基础较好的学生,可以在教学中给出完整的证明过程,甚至可以让他们自己寻找证明方法,以加深学生对定理的理解,扩展他们的解题思路;但对基础较薄弱的学生,即使给出证明,他们在理解上也会存在困难,所以这种补充只会增加学生的学习难度,并不利于他们对知识的理解与掌握.所以,教材对判定定理没有完整证明也是有正面影响的,如何把握教学,这需要教师的智慧.
从学生的角度,我也进行了了解.对于
“在学习立体几何中,你遇到的最大困难来自( )?
A.识图、认图(各元素间位置关系)B.推理证明
C.使用向量法时的计算 D.作图(三视图、直观图等)
E.其他_____”
这一问题的回答,学生中有7个人都选择了“推理证明”,其中还包括两名成绩优异的学生.他们表示,立体几何中的逻辑推理必须能够灵活运用其中的相关定理,虽然这些定理都知道,也都记得,但是在具体的题目中,并不十分清楚需要运用哪些,尤其是在一些中间过渡较多的题目中,有时就会出现无从下手的情况.不过,更让他们头疼的是如何添加辅助线,作出二面角的平面角.由此,我们可以看到,学生们对自己的逻辑推理能力是有怀疑的,他们也希望能在老师的帮助下得到加强.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




