教材作为新课程教学改革的重心和关键，其内容的编排，教师使用教材情况将直接影响新课程教学改革进程.通过对教材结构、教材例题、习题分析得出课程教学改革后教材编排符合学生心理认知发展需求，教材内容的严谨性对训练学生逻辑思维能力、解决问题能力具有重要意义.那么，在实际的一线课堂教学中，教师对教材使用情况如何？以下选取成都市某重点中学在解析几何“直线与圆的位置关系”这一课的实际教学片段为例进行分析：
师：我们一起回顾初中阶段的学习过程中直线与圆有哪几种位置关系？
生：相交、相切、相离.
师：很好，结合我们高中阶段学习的直线方程与圆的方程探讨相交、相切、相离有什么具体特点？
生：直线与圆相交时有两个公共点，相离时没有公共点，相切时有一个公共点.
师：很好，那么能否用直线与圆的方程探讨直线与圆的位置关系？如例子：2x+y=1 与x2+y2=1的位置关系是怎样判定的？
生（甲）：可以在直角坐标系上画出圆的图像、直线的图像，以此判定两者的位置关系.
师：这是一个好方法，但是作图很费时间，并且作图如果不精确会影响判定结论，除了作图以外，还有没有其他方法？
生（乙）：根据两图像交点的个数，联立直线与圆的方程消y，变为一个关于x的一元二次方程，判定Δ的大小.当Δ大于零时，说明直线与圆有两个交点；当Δ小于零时，说明直线与圆没有交点；当Δ等于零时，说明直线与圆有一个交点.
师：很好，这个方法直接从解析式出发，通过消元判定出直线与圆的交点个数，运用代数方法从解析式上入手判定，很简洁，简单，省去了作图不必要的麻烦，同学们一起判定2x+y=1 与x2+y2=1的位置关系？
生：Δ等于16，所以直线与圆有两个交点，即直线与圆相交，交点坐标通过计算得到为
（将行距调整为了40磅，也可以调节公式尺寸）(www.xing528.com)
师：很好，相信大家都会用联立方程组的方法判定直线与圆的位置关系，那么除了作图法和消元法以外还有没有其他方法？
生（丙）：根据初中学习知道，圆心到直线的距离大于半径，直线与圆相离；等于半径，直线与圆相切；小于半径，直线与圆相交，所以可以用点到直线的距离公式判定.
师：很好，圆心到直线的距离判定省去了消元法的复杂，只需找到圆心与半径即可，一步到位，那么同学们用该方法判定2x+y=1 与x2+y2=1的位置关系？
生：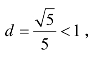
所以直线与圆相交.
师：通过以上两个例子分析，同学们一起运用高中知识判定直线与圆的位置关系的方法？
生：代数法，通过联立直线方程和圆的方程，直接判定Δ的个数，当Δ＞0时，直线与圆有两个交点；当Δ＝0时，直线与圆相切；当Δ＜0时，直线与圆相离没有交点.或者用几何方法，判定圆心到直线的距离，当d＞r时，直线与圆相离没有交点；当d＝r时，直线与圆相切有一个交点；当d＜r时，直线与圆相交.
师：同学们分别从几何角度与代数角度归纳总结出判定直线与圆的位置关系的方法.这两种方法各有其特点，遇到具体问题时要恰当选择合适的方法运用求解，现请看以下例题.
已知过点M(-3,-3)的直线被圆所截得的弦长为
求直线l的方程.（此时教室内同学们开始运用所学方法求解）
通过该课堂的实际考查看到，该教师在“直线与圆的位置关系”的实际教学中，以教材为背景，展开实际的课堂教学.教材在整个课堂教学中起主导作用，而且充分发挥其实际作用.与此同时，在“直线与圆的位置关系”课堂教学中，该教师摒弃了以往平铺直叙的教学方法，而是以初中阶段直线与圆的位置关系的判定为线索，通过循循善诱过渡到高中阶段“直线与圆的位置关系”的判定，最后通过一系列的归纳、总结得出以初中知识为背景，判定“直线与圆的位置关系”的方法.整个课堂教学过程中，教师通过“问题串”将本节内容有机串起来，形成明确的教学主线，学生能够在教师“问题串”的自然引导下完成对课程内容的探索，并且在知识学习过程中经历假设、猜想、论证、归纳等一系列心理活动，由此对新课程的内容学习更加根深蒂固.
课程教学改革后，教材编写充分展现出对问题情景的呈现以及前后知识的相互联系.对知识采用螺旋式上升的编写特点，更符合学生的认知心理学.与此同时，教材在编写时更加注重对学生数学思维以及数学能力的培养，实际教学过程中更注重培养学生将课本知识运用到实际生活中的能力.因此，与以往老教材编写相比较，对于现行教材，教师在实际课堂教学过程中展开以教材为依托的教学更加顺利，对课堂整体把握度更加明确，学生的实际学习效果也比较突出.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
