解析几何教学案例分析-高中数学实践研究

影响高中数学课程改革的因素是多方面的，其中教材编写直接决定高中数学课程改革的成败.教材在课程改革中起奠基作用，课程改革的最终形式以数学教材的形式呈现出来，教师以教材为媒介将数学知识传递给学生，学生则以教材为起点展开数学课程的学习.课程教学改革后，教材编写注重知识的层次性与连贯性，教材内容的选择突出数学来源于生活并运用于生活的本质特征.概念与定义、例题、习题组成高中数学教材，此次课程改革后解析几何部分的教材在例题的编排与习题的选择上都经过编者反复论证与精心设计，其根本目的就是推进高中数学课程改革的成功.下面将选取高中数学课程改革后解析几何教材例题、习题调整案例来分析课程改革后的教材编写情况.

1.解析几何教材例题调整案例分析

例题在数学教材中是连接定义、定理和习题的桥梁，学习新概念、定义、定理等内容后例题是对这些新知识的最直接呈现形式.高中数学课本中的例题经过编者精心设计与精心编排，每一道例题都具有典范性，同时每一道例题中均蕴含基本的数学思想与数学方法.例题对教师的教学有指引作用，通过例题的展示，可以加深学生学习新知识的理解；学生也可以通过例题巩固新概念和新定义，以此达到两者间相互共鸣的目的.

原有教材中例题强调当节内容，当节知识点在例题中反复出现，让学生通过机械操作与反复记忆来巩固新内容.课程教学改革后，解析几何教材在例题选取与编排上突出新课程教学改革的理念，例题紧密联系知识主线的同时也强化对知识的灵活运用，同时例题中更注重学生数学思维与数学创新精神的培养，极大限度地提高了数学课程的教育价值.

例如，原有教材中关于“直线与直线平行”有如下两道例题：

例1：已知直线方程l1:2 x-4 y+7=0,l2:x-2 y+5=0，求证l1//l2.

例2：求过点A(1,-4)且与直线2 x+3 y+5=0平行的直线方程.

这两道例题均突出直线与直线平行这一主观条件.其中，例1通过两条直线的一般方程来判定12//l l，直接判定是条件的迁移；例2则间接利用直线与直线平行这一前提求解方程.两道例题的目的明确，直奔直线与直线平行这一主题，学生可以通过例题进行模仿训练并强化记忆直线与直线平行这一知识点.

而现行教材中“直线与直线平行”例题的呈现方式与之前有较大区别，如以下两道例题：

例3：已知A(2,3),B(-4,0),P(-3,1),Q(-1,2)，试判断直线BA与PQ的位置关系，并证明你的结论.

例4：已知四边形ABCD的四个顶点分别为（A0，0）,B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状，并给出证明.

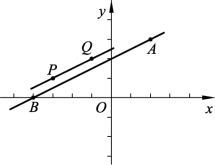
例3图

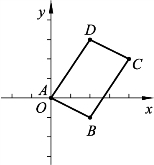
例4图

例3分别给出A,B,P,Q四点的坐标，以此来判定直线BA与PQ的位置关系.题目中没有明确说明直线BA与直线PQ的平行关系，学生首先会对两直线的位置关系进行猜想，进而进行验证.学生通过求出直线BA与直线PQ的斜率，再利用当堂课上直线与直线平行的判定条件可以解出该题.例4则在例3的基础上进行变形，通过给出四边形四点的坐标来判定四边形形状.鉴于例3的学习，学生会求解出直线AB,BC,CD,AD的斜率，根据两组对边斜率分别相等判定出四边形ABCD的形状.

例3、例4的解题结果均以直线与直线平行的判定条件为依托，让学生学会判定和运用直线与直线平行这一核心概念；但是例题的呈现方式不同于以往教材中直奔主体，并机械记忆.这两道例题均给予学生思考空间，然后从脑海中整合出最合理的解题方案，最后运用到例题解答中.例题设计不再是以往一看就明白解题方向，一看就知道解题知识点，这样的设计无疑诠释了新课程教学改革后转变学生死读书、读死书的现状，进而培养学生思维的灵活性与创新性.

课程教学改革后，解析几何不仅在例题设计上凸显灵活性与创新性，也在例题难度编排上略有降低，如“直线与圆的位置关系”有以下两道例题：

例 1：如例1图所示，已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2 y-4=0，判定直线l与圆的位置关系；如果相交，求它们的交点坐标.

例2：已知过点M(-3,-3)的直线l被圆x2+y2+4 y-21=0所截得的弦长为，求直线l的方程.

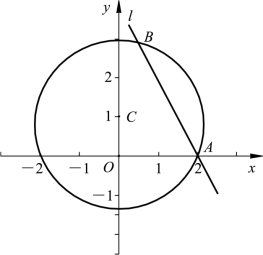
例1图

例2图

“直线与圆的位置关系”是新课程教学改革后加入的新知识点，课本对该节内容的安排是通过例题运用和求解来找出直线与圆的位置关系.学生在学习该节知识过程中，通过经历对例题的感知、认识、求解等一系列活动最后得到直线与圆位置关系的求解方法.例1、例2的设计都紧扣直线与圆位置这一主题，难度上均符合学生学习需要，学生可以通过对知识的理解与探究得出相应的结论，这无疑增加了学生学习的积极性与热情.

通过以上案例分析得出，课程教学改革后教材在例题选取上反映数学的本质，同时充分考虑了学生的认知水平与心理特点，例题选择呈现基础性、典型性、多样性、生活化等特点，这样不仅培养学生的数学思维并提高学生的学习兴趣，同时培养了学生将数学知识运用到实际生活的能力.

2.解析几何教材习题调整案例分析(www.xing528.com)

课程教学改革后，数学教材在概念与定理、定义、例题、习题三个板块均进行较大改变.通过现行与以往教材的对比，新课程教学改革后，教材在习题形式、功能、价值取向上均较准确地把握了课程改革的内涵，突出了数学的本质，体现了数学与实际生活的联系，培养了学生的创新能力.

在教材中有两种呈现形式：第一、每节内容的课后练习题；第二、每一章内容后的总练习题.每一节后的课后练习题一般是针对该节内容设置，其目的是强化本节内容的学习，一般有三至五道题；每一章的课后练习题是对一章内容学习的整合，目的在于考查一章内容的学习效果，题目更具典范性.现行教材与以往教材在习题编排、数学内容及题型等几个方面均有较大差异，现选取“圆的方程”该章习题为例进行分析，如表4-18所示.

表4-18　“圆的方程”习题数量统计

由表4-18中的数据分析可知，新课程教学改革后，“圆的方程”此章习题类型与老教材基本相同，但是每个类型的习题数量明显多于老教材习题数量，其中判断题、画图题、其他类型与老教材数量差距较大.以上三种类型题目增加的目的在于培养学生严谨的数学思维，让学生通过一系列的独立思考来培养其解决问题的能力，同时防止学生将数学课程变为单纯的机械模仿与记忆活动，违背数学原有的本质精神.

除了表4-18中的习题数量对比外，新课程教学改革后，解析几何习题还突出课改理念，主要体现在以下几方面.

（1）习题选取应生活化，体现数学来源于生活，运用于生活的本质.

数学的本质来源于生活，并且回归于生活.课程教学改革的目标之一是培养学生应用数学解决实际问题，此次教材在习题选择上很好地诠释了这一主旨.

例如，教材选修1-1中习题2.3第6题：图4-7（b）中是抛物线形拱桥，当水面在l处时，拱桥离水面2 m，水面宽4 m.水面下降1 m后，水面宽是多少？

图4-7

图4-8

再例如，必修4中4.3.2的练习题：赵州桥的跨度是37.4 m，圆拱高约为7.2 m，求这座圆拱桥的拱圆方程（见图4-8）.

相比较原有教材中习题强调对知识机械模仿与记忆的特点，增加这样的类型题是新课程教学改革后数学教材展现的突出点.此类习题拓宽了学生的数学视野，教会学生应用所学知识解决实际问题，以增加他们的社会实践能力.

现行教材在习题选择上很多是基于学生已有的数学知识和生活经验，通过将两者较好的融合，来培养学生运用数学知识解决实际问题的能力.

（2）习题选取应注重基础性，强调数学知识的来源与形成，注重培养学生的数学思维.

此次数学课程改革的目标之一：“让学生理解知识的发生、发展过程”.此目的是改变原有机械、死记硬背的形式，让学生从自我认识和自我感知的情况下，了解知识的来龙去脉，体会其中蕴含的数学思想与数学方法，从而培养自我的逻辑思维能力.

例如，必修2中习题4.1A组第6题：平面直角坐标系中有A(0,1),B(2,1),C(3,4),D(-1,2)四点，这四点能否在同一圆上？为什么？求解该习题的前提条件为明确形成圆的条件与四点共圆的条件，然后才能判定.如果没有对圆概念与条件特别清晰的思维，该习题就无法求解.

同样类型的习题也出现在B组：长为2a的线段AB的两个端点A和B分别在x轴和y轴上滑动，求线段AB的中点轨迹方程.

关于此类型习题，要抓住数学问题的本质，只有清晰地掌握数学知识的形成过程，才能顺利解答.通过该类型习题可以培养学生严密的数学逻辑思维，这与课程改革的主旨相呼应.

（3）习题选取应注意与其他学科的内在联系，拓宽学生的数学视野.

数学不是一门独立的学科，其他学科的发展离不开数学的奠基作用，同时其他学科也促进数学学科的发展.老教材中数学内容较为单一与独立，缺乏与其他学科之间的联系，而新课程教学改革后，教材编写恰好弥补了这一缺憾.例如，教材编写注重与现代多媒体信息技术的联系与结合.在解析几何该部分，尤其强调几何画板的运用，如选修1-1习题2.1例子.

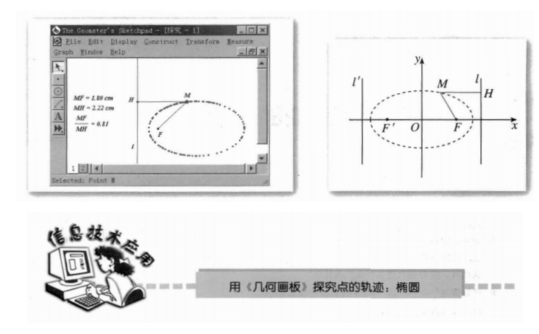
运用“几何画板”探究点的轨迹：椭圆.通过图形生成形式，生动、形象地展示椭圆的形成过程，让学生达到视觉上的认知，以强化对知识的理解.同时学生也可以实际动手操作演示椭圆的形成过程，进一步加强对知识的理解.

通过以上习题案例，分析得出现代信息技术与数学学科的紧密联系，强化了学生的学习，拓宽了学生的数学视野，让学生从本质上认识数学不再是一门学无所用的学科，间接增加了学生学习数学的兴趣.

此次课程教学改革后，教材在习题、例题的编排上虽然以传统题为主导，但是在习题、例题选取上又有新的突破.例题注重基础性、创新性，习题强调数学逻辑思维训练，加强与其他学科的内在联系，同时两者均强化数学与实际生活紧密联系这一主旨，以增强学生的实践能力.