1.教师在没有极限情况下的教学行为
问题19是调查教师在“没有极限”情况下讲导数的教学行为现状.教材选修1-1中导数及其应用部分,开篇就是变化率(气球膨胀率、高台跳水)问题的教学,之后通过“瞬时速度”到“瞬时变化率”的变化过程引出导数概念,没有涉及极限知识.关于“舍弃极限”讲导数,这是大多数教师在导数教学时都会遇到的问题,因此,如何进行教学处理,是我们一线教师的重中之重.
表3-21 无“极限”情况下教师的教学行为

在3.4.2(3)部分中,通过第10题我们已经研究了教师对没有“极限”讲导数的认知状况,大多数教师认为在有极限的情况下导数内容会更好教.从表3-21中的数据可以看出,有42.9%的教师会先引入极限,再讲导数,而39.2%的教师不会这样做,还有少部分(17.9%)教师是不置可否的.这说明还是有很大一部分教师认为在有极限的情况下更有利于导数的教学,所以在实际的课堂教学中,他们也会通过引入极限来引导学生,然后再给学生讲解导数知识,他们在新课改的教材知识基础上加入了自己的教学设计.而另一部分教师则按照新课改的教材内容来进行实际教学,不会给学生先讲极限,然后再讲导数知识,而是把导数当作一个特殊的极限来讲,这减轻了学生学习导数的负担,更容易保持学生的学习兴趣.为进一步探究各因素在第19题选择差异的影响,分析导数教学中具体的影响因素,我们对此题与各因素之间的影响做了卡方检验,其结果如表3-22所示.
表3-22 无“极限”情况下教师的教学行为差异的影响因素
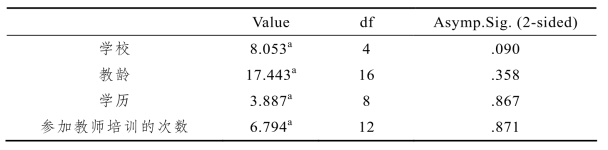
从表3-22中卡方检验的数据可以看出,无论是教师的学校、教龄、学历,还是参加教师培训次数(p>0.05)等各因素,对无“极限”情况下教师的教学行为都没有显著性差异.这说明持不赞成或者不置可否态度的教师在处理无“极限”情况下的导数教学时更多的是其他原因,比如学生的学习情况、课标的要求等.即在没有“极限”的情况下,教师可以把导数当作特殊的“极限”来进行教学,用导数这个特殊的“极限”来让学生体会“无限”的思想.
2.教师在导数教学时的具体教学行为
问题20,21主要调查教师在导数内容教学实践中,对知识的引入,以及学生的知识准备这两个问题如何去处理,其统计结果如表3-23所示.
表3-23 在导数内容教学时的具体教学行为(https://www.xing528.com)

从第20题的统计结果可以看出,73.1%的被试者没有持反对态度,其中32.1%的教师持不置可否的态度.这说明很大一部分教师在导数内容教学过程中,会适当引入微积分的发展史,或者关于微积分的趣事,等等.从21题的统计结果也可以看出,71.5%的被试者没有持反对态度,这与第20题的73.1%的结果大致相同.这足以看出大部分教师对课前准备以及课堂引入的重视程度.微积分具有悠久的发展史,无论是国内还是国外,微积分的发展都有很好的文化积淀和历史延革,这些辉煌的成就足以激发学生的学习兴趣,让他们对接下来的导数学习产生浓厚的兴趣.要求学生在课前去查阅关于微积分、导数的资料,不仅可以提高学生的学习兴趣,为后续学习做好知识储备,还可以培养学生良好的学习习惯,这是学生发现问题和提出问题的有效途径.新课标教材在“探究与发现”中给出了“牛顿法:用导数方法求方程的近似解”以及实习作业“走进微积分”,其中实习作业“走进微积分”可以在新课讲解之前就要求学生按时按质的完成,教师可以根据学生的完成情况进行奖惩.
3.教师对于导数“工具化”的处理情况
问题22是调查教师对导数“工具化”与实际应用的处理情况,其统计结果如表3-24所示.
表3-24 对导数“工具化”的处理情况

从统计结果可以看到,持赞成态度(46.4%)的多于不赞成(34.0%)的人数,即有一定比例的教师并没有完全把导数当作学生的解题工具来教学,而是兼顾学生思维能力和实践能力的培养.而在持赞成态度的教师中,有一部分教师在实际的教学过程中,往往偏重应试教育,因为导数是解决函数问题的一个有力工具,认为能应用导数的计算公式来解导数方面的题型就可以了,不注重学生“无限”思维的培养,忽视导数与学生生活实际之间的联系,一味地迎合应试教育.导数作为解决函数问题的有力工具,在解决函数问题时可以使计算简便快捷,特别是解决非基本函数题型,确实需要学生掌握导数的计算公式并提高计算能力,且能用导数来解决函数问题,如用导数的正负来判断函数的单调性,再通过函数的单调性来求函数的极值等.随着导数工具化在高中数学中的普及,高等数学思想也慢慢渗透到高中数学的解题之中,其中,导数和方程式、数列、不等式以及解析几何等相互交汇来进行命题,以达到考查学生学习数学能力的目的.因此,我们更应该强调微积分的基本思想和应用方法,这种非形式化的教学是将导数成功引入中学教学课堂的保证,同时也培养了学生探索实际问题的能力.统计结果中有53.6%的教师持不赞成或者不置可否的态度,其中5.4%的教师持很不赞成的态度.我们对此问题的差异影响进行了卡方检验,为找出具有较大差异的原因,将卡方检验结果填写于表3-25中.
表3-25 导数“工具化”处理情况差异的影响因素
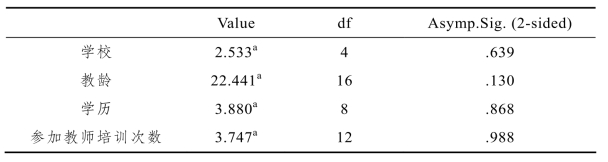
从第22题的各因素的卡方检验可以看出,教师的学校、教龄、学历、参加培训次数(p>0.05)等因素在将导数当作解题工具来进行教学的处理上不存在显著性差异.这说明高中数学中,导数的“工具化”问题与用导数解决实际问题的关系的认识在大多数学校是普遍一致的,特别在新课改下,教师对导数的实际应用也重视起来了.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




