高中数学教学：三角函数定义的比较

原有教材采用的是终边定义法，即“正弦、余弦、正切、余切、正割、余割都是以角为自变量，以比值为函数值的函数，以上六种函数统称为三角函数”．其优点是进行三角函数求值运算时简单快捷.然而三角函数的所有性质、图像和公式的推导，都是借助于单位圆得出，但原有教材却没有明确单位圆在三角函数学习中的中心地位，致使很多学生忽略了单位圆在三角函数学习中的重要性.而三角函数内容的一个典型特点就是公式繁多复杂，那么怎么才能记住这么多的公式呢？这也是大部分学生害怕学习三角函数的一个很重要的原因.而在现行教材中，采用的是单位圆定义，即“正弦、余弦、正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，我们将它们统称为三角函数”．这样就明确提出了单位圆在三角函数学习中的中心地位，引导学生借助单位圆的直观，去探索三角函数的性质、公式以及图像的来龙去脉.这样一来，学生会在头脑里形成一个以单位圆为中心的知识网络，便于理解和记忆.同时，现行教材采用单位圆定义，还有许多其他好处.

高中数学教师在进行函数定义教学时，都会着重强调函数满足的是“一一对应”和“多对一”法则.另外，我们在书写函数表达式时，习惯上都是以x为自变量，y为因变量.但是，如果采用“终边定义法”，则正弦余弦都是以比值为函数值.如图2-1所示.

设P,P1,P2,…都是角α终边上不同位置的点，则

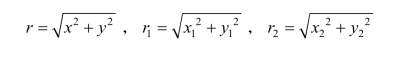
图2-1

由终边定义可得到

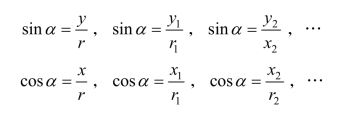
函数定义对高一学生来说是一个难点，一部分学生根本就没有真正理解其中的含义.在这里，老师如果处理不好，或者学生没有认真听课，很容易引起这样的误会，即一个α，同时有多个函数值与之对应，即“一对多”问题.然而从高中函数定义的角度来看，它根本就不是一个函数，这样就容易引起学生认知上的混乱.而现行教材中用单位圆来定义三角函数：sinα=y,cosα=x，就很好地避免了这种情况的发生.因为单位圆上的任意一点的坐标都是独一无二的，即每一个α都只有唯一的一个x或y与之对应，这很好地符合了高中对函数的定义，学生们接受起来比较容易.

《普通高中数学课程标准》中对三角恒等变换等传统三角函数内容进行了精简，同时还对一些内容降低了学习要求.其目的就是突出三角函数作为描述现实世界中周期运动的数学模型的本质.周期性是三角函数的第一性质.原有教材仅仅是从代数角度来说明周期性的，即由诱导公式sin(α+2k π)=sinα，cos(α+2kπ)=cosα(k∈Z)，来推导出正弦函数、余弦函数的周期性.而现行教材不但用了诱导公式来说明正弦函数的周期性，还强调在前面的学习中，教师要引导学生通过对正弦线的变化规律的观察，来体会正弦函数值的“周而复始”的变化规律，让学生直观地“看见”正弦函数的周期性，达到数形结合的目的.这样学生的理解会更加透彻，印象也更加深刻.新课程提倡积极主动、勇于探索的学习方式，这一点在现行教材中体现得淋漓尽致.现行教材只是推导了正弦函数的周期，然后让同学们自己去探索余弦函数的周期.采用单位圆定义后，学生就会很自然地利用单位圆中三角函数线的直观形象去探索余弦函数的周期，大大降低了探索的难度，对于观察、探究和分析等数学能力并不强的高一学生而言，这无疑会更加符合他们的实际情况.而且通过对三角函数的数和形两方面的研究，学生能够知道知识的来龙去脉，并且体验再创造数学的乐趣，从而激发学习数学的兴趣.

我们学习新函数，都是从函数的图像和性质（定义域、值域、单调性、奇偶性）等方面着手去研究.采用终边定义法，如果要求三角函数的定义域和值域，还要经过一系列的运算，比较麻烦.而采用单位圆定义法，则可以在图像上，利用三角函数线，将其定义域、值域、单调性直观地展示出来，较好地体现了知识的来龙去脉，容易被学生接受，可以克服他们学习三角函数时的恐惧感.

比如求三角函数的值域、单调性等性质，我们也可以通过单位圆的三角函数线的变化规律，直观地展示出来.下面以正弦函数为例，如图2-2所示.

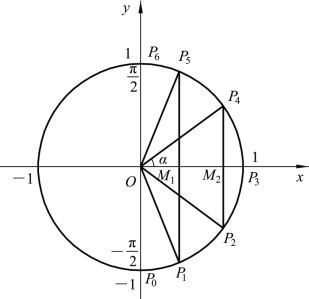
图2-2

当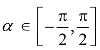时，从图像中角α的正弦线

(www.xing528.com)

的变化趋势可以看出：

当α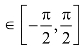时，随着角α的增大，其正弦值sinα也在逐渐增大；

当α=时，sinα取到最小值1-；

当α=时，sinα取到最大值1.

当α∈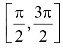时，由

的变化趋势可以看出，随着角α的增大，sinα的值反而减小（见图2-3）；

当α=时，sinα取到最大值1；

当α=时，sinα取到最小值1-.

所以当α∈[0,2π]时，-1≤sinα≤1.

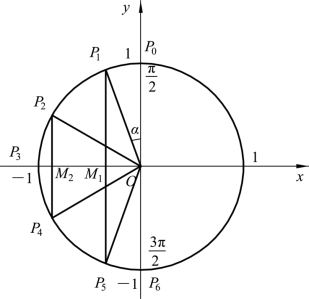
图2-3

再根据单位圆的周期性，我们可以得到：当α=2kπ-时，sinα取得最小值1-；当α=2kπ+时，sinα取得最大值1.

所以正弦函数的值域是[1,1]-.

同时，借助单位圆的直观，还可以引导学生初步了解正弦函数的单调递增区间是单调递减区间是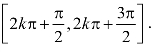

综上所述，我们可以深刻体会到单位圆在三角函数学习中的重要作用，以及现行教材采用“单位圆定义”的必要性.