问卷的第17~23题,是对作为函数模型的数列的问卷调查,旨在了解教师对数列在高中数学中的地位和作用的认知情况,以及对新课标提出的新的教学目标和内容要求是否熟悉.其中,第17,19,23题是调查教师对数列模型的课程观;第18,21,22题是调查教师对数列模型的教学观;第20题是调查教师对数列模型的应用价值观.调查结果如表1-12所示.
表1-12 教师对数列模型的教学认知百分数表
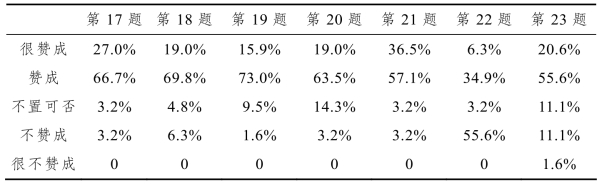
根据表1-12中的数据,我们可得到以下结论:
(1)对第17题,有93.7%(27.0%+66.7%=93.7%)的教师赞成数列是高中数学的一个知识重点,也是教学难点;对第19题,有88.9%的教师认同数列是一种特殊的离散函数,这可以帮助学生进一步认识函数的本质;而对第23题,有23.8%(11.1%+11.1%+1.6%=23.8%)的教师不认同或不能深入理解“等差数列是一次函数的离散形式,等比数列是指数型函数的离散表示”,这对学生来说很重要.
这说明,大多数教师对数列在新课程中的地位和作用是清楚的,对数列是一种特殊的函数也是高度认可的;但少部分教师对“等差数列与一次函数、等比数列与指数型函数的关系”的认知程度较低.
(2)对第18题,有88.8%的教师认同对数列可以从函数角度来进行教学,而对第22题,又有41.2%(6.3%+34.9%=41.2%)的教师是赞成数列与函数的关系需分开讲,以免学生感到混乱.这里,部分教师出现了认知上的冲突.对第21题,93.6%的教师赞同在数列教学中应从生活实例中引出数列概念.
这说明,绝大多数教师都认为应从数列的生活背景中,创设情景,引出数列概念.这与《普通高中数学课程标准》提出的新教学理念:“要体现数学的知识背景”是相一致的;而对数列的教学处理,可能会存在多种教学方式:有的会从函数范畴来教,有的会从数列角度来教,或有的从函数与数列交叉点来教,等等.
(3)对第20题,有14.3%的教师不清楚可以用数列模型来解决日常生活中的许多问题.
这说明,这部分教师对数列的应用价值不够清楚或没有重视.数列模型的原型来源于我们的生活和生产中;反过来,又可以用它去解决我们生活中类似的问题,并且这些问题在生活中是常见的,如教育储蓄、购房贷款、人口增长、考古年限等问题.让学生用数列去解决这些问题,参与数学建模的过程,体会其中的数学思想方法,有助于提高学生学习的积极性,使其感受学习数列是很有用的.
为进一步探究以上结论与教师的教龄、职称、学历等因素是否有显著性关系,我们又做了相关的卡方分析(见表1-13).
表1-13 关于数列的课程观、教学观以及应用价值观的相关结论的卡方检验
 (https://www.xing528.com)
(https://www.xing528.com)
从表1-13中的数据,我们进一步得出以下结论:
(1)教师对“数列在生活中的应用价值”的认知程度与教师的教龄、职称、学历和所教班级人数都无显著性关系.这说明此问题受教师的个人专业素养影响较大.
(2)不同教龄、不同职称、不同学历的教师对“数列与函数”的教学处理存在显著性差异.我们可对第22题与教师教龄和学历的交叉表(见表1-14和表1-15)做具体分析.
表1-14 第22题与教师教龄交叉制表
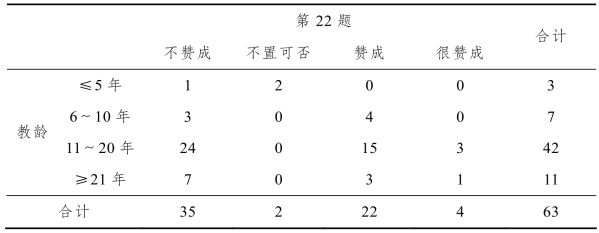
从表1-14中的数据可知:在不赞成“数列与函数的关系要分开讲”的教师中,教龄在5年及其以下的教师中约占2.8%、6~10年的教师中占8.6%、11~20年的教师中占68.6%、21年以上的教师中占20%.可见,随着教龄的逐渐增长,持不赞成的比例会越来越高,但到了一定年限(20年),持不造成的比例又会下降,这说明他们对数列教学的认识随着教龄的增长会更加深刻,处理得也会更加合理、更加恰当.当然,对于超过20年的教师,这可能与他们的知识老化有关.
表1-15 第22题与教师学历交叉制表
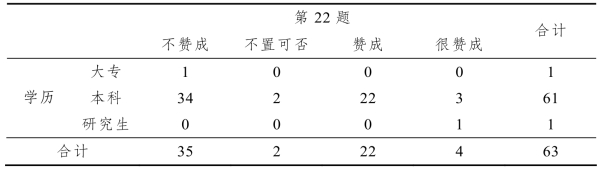
从表1-15中的数据可知:研究生学历和大专学历的教师各一名,在统计学上不具有代表性,所以他们的选择不宜参考.但这也从侧面反映出,高中数学教育还紧缺高学历的教师人才.因此,为了提高教师的教学理论水平和教研水平,还需鼓励教师继续学习.而从本科学历的教师中,也可明显地发现教师对“数列的教学处理方式”存在严重分歧.
(3)教师对“等差数列与一次函数、等比数列与指数型函数之间的关系”的认知程度与教师所教班级的人数有显著性关系.我们可对下面的交叉表(表1-16)做具体分析.
表1-16 第23题与班级人数交叉制表
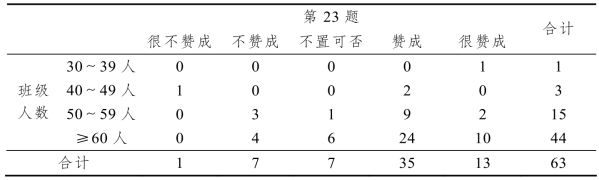
从表1-16中的数据可知:授课班级人数在49人及其以下的教师极少,大多数教师授课班级人数在60人以上,而大班级授课的教师中,近4/5的教师认为学生深入理解“等差数列与一次函数、等比数列与指数型函数”之间的关系是非常重要的,这能帮助学生更好地理解和掌握等差、等比数列.这也说明,虽是大班级教学,但教师对数列教学的认识还是较为准确和深刻的.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




