函数是高中数学中的一个核心概念.人类对函数的认识经历了一个漫长曲折的过程，由具体到抽象、由模糊到准确，逐步形成一个更加抽象和精确的认识系统.
函数的一般概念虽在17世纪形成，但函数的思想，早在原始社会，伴随着人类的生产也就产生了.例如，中国的结绳计数，就是“一一对应”函数思想的体现.在经历了漫长的岁月之后，人们对函数的认识有了更加具体的体现.在14世纪，法国奥雷斯姆（N.Oresme）运用曲线来表示速率与时间之间的关系，到了17世纪，函数更多的则以曲线形态呈现出来，这就是函数的早期认识形态.
直到1673年，德国数学家、哲学家莱布尼兹（G.W.Leibniz）在他的手稿里最先用“function”一词来表示任何一个随着曲线上的点的变动而变动的量.1692年，他第一次明确给出了函数定义：“像曲线上的点的横坐标和纵坐标、切线的长度、垂线的长度等，这些所有与曲线上的点有关的量，即称为函数.”这时的函数已经蕴含了一种依赖关系.
到1718年，瑞士数学家约翰·伯努利（Johann Bernoulli）打破几何思想的束缚，把函数定义为：“变量的函数是由这个量和常量组成的解析表达式”，即函数就是解析式.这是对函数认识的第一次升华.
瑞士数学家欧拉（Leonard Euler）于1734年，首次使用“f()”来表示函数.为使函数概念适应积分的需要，在经历了一番探究和研究后，他对函数有了新的认识.于1755年他这样写道：“如果某些量以某种方式依赖于另一些量，而当后者改变时它也发生某种变化，则称前者为后者的函数.”这是从“变化说”或“依赖说”来认识函数的，是对函数认识的第二次升华.
法国数学家柯西（Cauchy）对函数的认识是：“对于x的每一个值，如果y都有唯一确定的值与之对应，则y叫作x的函数”.此定义中，把用分段解析式表示的关系式纳入函数定义中，基本上摆脱了“解析表达式”的要求，它侧重于关于变量间关系的认识.也就是说，到18世纪末，人们把函数拓展到了“分段函数”.这是对函数概念进行的第三次扩充.(www.xing528.com)
1807年，法国数学家、物理学家傅里叶（Fourier）发现一个函数可以表示成一个无穷三角级数.1812年，高斯（Gauss）把超几何级数作为函数，其表达式是无穷级数.这就是我们在高等数学中认识的函数：“函数在某点可展开成一个无穷多项式.”
直到1837年，德国数学家狄利克雷（Dirichet）给出新的函数定 义：“如果对于给定区间上x的所有值都对应着完全确定的y值，则称 y是x的函数.至于用怎样的方法建立所指出的对应关系并不重要.”这就是人们常说的经典函数定义,他还给出一个著名函数例子：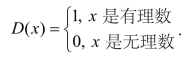
这是对函数认识的第四次升华.
19世纪70年代，美国维布伦（Veblen，1880—1960）用德国康托尔（Cantor）的“集合论”给出了近代函数的定义.此定义打破了“变量是数”的限制，强调对应关系的存在性，也就是高等数学中所指的“泛函”，它使函数的概念更为抽象，更加完备.这实现了对函数概念的第五次扩充.
20世纪中叶，“函数就是一种关系”是对函数更广泛的认识，这是对函数认识的第六次升华.
综上所述，历经三百多年，对函数的认识，大体经历了：“图像”→“解析式”→“依赖说”→“对应说”→“关系说”，同时也适应了数学学科自身的发展要求和社会科技发展需求，展现和凝聚了无数数学家们的科研成果和智慧.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
