1.普通最小二乘法模型(OLS)
普通最小二乘法的研究经历了几代人的发展,最早由Johnson(1960)和Stein(1961)提出使用期货价格序列与现货价格序列作为自变量和因变量,接着Ederington(1979)通过研究发现使用期现货价格的差分序列效果更佳,在此基础上Brown(1985)进一步创新性地提出将期现货价格的收益率作为因变量和自变量。在此之后国内外的实证研究中,普通最小二乘模型较多地使用收益率序列作为变量。本章也参照该种方法,估计结果如表7.7所示。
表7.7 OLS最优套保比率估计结果

从表7.7的估计结果中可以发现,在显著性检验中,铜日数据、周数据的β系数概率值P均为零,这说明β系数显著,不能拒绝原假设。由最小二乘法的模型设定可知,β的估计值即为最优套期保值比率h*的估计值,故本次实证研究中应用OLS模型得出的日数据套期保值比率为0.637 517,周数据套保比率为0.883 938。分析实证研究的结果可以看出,周套期保值比率大于日套期保值比率。这是由于在一般情况下,套期保值周期越长相应价格波动的幅度越大,故计算得出的套期保值比率也就越大。但由最小二乘法估计得出的套期保值比率并未考虑两个价格序列之间的协整关系,忽略这样的关系极容易产生伪回归,即当两个序列相关性不大时,仍能产生很好的回归效果。
2.误差修正模型(ECM)
在前面的协整检验中,已证明两个价格序列存在协整关系,可建立误差修正模型。由表7.4和表7.5可知日现货价格对期货价格的回归系数为0.891 774,周期货价格对期货价格的回归系数为0.887 814,因此建立误差修正项:
Ecm1=S(-1)-0.891 774*F(-1)
Ecm2=WS(-1)-0.887 814*WF(-1)
使用Eviews进行回归,结果如表7.8、表7.9所示。
表7.8 日数据误差修正模型估计结果(https://www.xing528.com)

由表7.8可知误差修正模型的估计结果为:
ΔS=1 329.729+0.656 723ΔF-0.224 359Ecm1+μ1
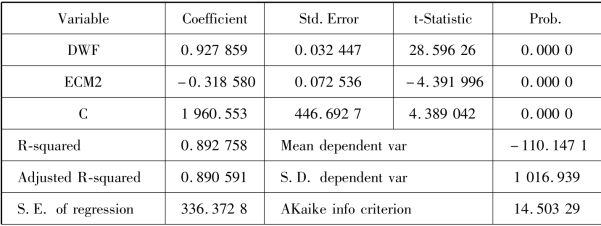
表7.9 周数据误差修正模型估计结果
续表
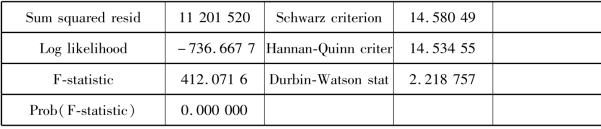
由表7.9可知误差修正模型的估计结果为:
ΔWS=1 960.553+0.927 859ΔWF-0.318 580Ecm2+μ2
在这里,ΔS为日现货价格的差分,ΔF为日期货价格的差分,ΔWS为周现货价格差分,ΔWF为周期货价格差分,Ecm1、Ecm2分别为误差修正项,μ1、μ2分别为随机误差项。
从以上两个误差修正模型的估计结果可知:两个回归方程的F统计量在整体上是显著的,自变量系数和误差修正项系数的t统计量也是显著的,由此可以推断,方程的回归拟合效果都比较好。另外从模型估计结果中可以推断出,当铜相关企业拥有一个单位的现货头寸,在期货市场上就需要用0.656 723个单位期货头寸进行对冲,即日套期保值比率为0.656 723。同理可知周套期保值比率为0.927 859。分析误差修正模型的实证结果可知,套期保值的时间周期越长,价格波动幅度越大,套期保值比率也就越大。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




