基于深度学习的高中数学教学研究：分析学生数学认知起点

（一）分析学生认知起点的策略

基于约翰·比格斯的理解，数学认知就是指学生对于所接收到的数学知识、数学经验等进行判断、储存、提取和使用的一系列信息加工过程，是对数学客观事实的一种认识活动。

具体来说，分析学生数学认知程度，就要了解学生数学认知起点，即已有的数学知识架构和自然生活经验，例如初中学习过函数的概念，高中则将映射这一理念教给学生，是概念的完善，之间的过渡教师就应该好好斟酌。要想充分利用数学认知起点来达到深度学习的目标，就要完成下面几个步骤。

第一步，了解高中生认知发展规律。高中生在学习过程中从无意记忆、机械记忆向有意记忆、理解记忆发展，认知结构在不断地完善。数学的认知水平是指学习者通过对外显性经验和感知转化为自己可消化的知识的水平，高中生的数学认知基础来自初中及之前原有的数学经验，在高中学习中，学生的认知较为稳定，可以将注意力放在烦琐的数学知识中去，且认知比较全面，乐意去评论别人的意见和发表自己的见解。高中生已具有较为良好的自我认知，可以客观地看待自己的数学水平，发现自身的不足，进行自我调节。

第二步，立足学生，了解认知起点。数学的教学必须重视学生的认知起点，这是深度学习的基石，也是教学的基石。教师可以通过学生课前小测进行学生认知水平的分析，可以进行几个水平小测试或是让学生尝试着画一些维恩图将自己所具有的认知结构展示给教师，在此基础上，教师进行知识迁移或者知识建构的巧妙设计。

第三步，对班里学生程度分布进行分析。最近发展区和“支架式教学”都立足于所有学生的共同发展，每个班里学生的层次参差不齐，教师要想让每个学生都在数学课堂中有好的体验，就得学会让学生发挥其主观能动性。设置学生感兴趣、有挑战的主题，让其感受认知的不平衡，激发学习兴趣。心理学家曾研究一个人的动机强度与学习效果间的关系。

当学生在学习新的知识时，若知识水平过于简单，则无法很好地激发学习动机；若难度适中，则学习动机与学习效果成正比；若知识水平过于难，与自己所具备的认知水平间差异过大，会影响学生的学习动机，容易因为无法获得良好的数学体验和挫败感而放弃理解知识，这时学习效果也会变差。教师应在前期对班里学生个性、能力水平分布和家庭背景等其他因素进行掌握，设计课程时不仅要注重学习程度好些的学生的学习体验，也要兼顾思维缓慢的学生，进行教学平衡，难度适中，这也是教学预测中的一个要素。

第四步，关注课堂中学生的疑惑点、兴趣点和生成点。教师要角色互换地站在学生的角度去重新审视知识内容，找到缄默点，思考学生在哪些地方容易产生疑问，这也是批判性学习的关键点，教师要提前预设如何处理学生的疑惑之处，使学生自然生成对新知的接纳。深度学习追求通过循循诱导激发学生产生兴趣，自觉参与到问题的探究中，也就是要关注学生的情感体验，使知识变得立体和生动。

这方面学情的判断对新教师或许存在一定的困难，所以可以向有经验的教师进行请教，也可以利用第一步的导学案或课前测验进行针对性的分析。

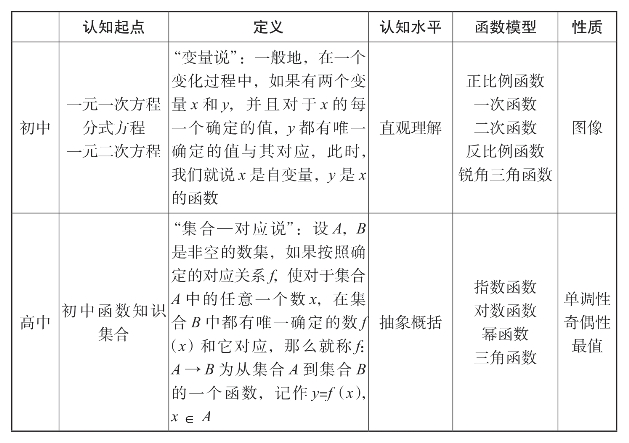
函数在初高中教学中就需要考虑学生的认知起点，表3-2展现了函数知识在不同学段下的相关变化。

表3-2　函数认知发展(www.xing528.com)

（二）分析学生认知起点的课例：《函数》的教学片段

1.函数的概念

回顾：初中时学习的函数定义。

思考：y=x，是同一个函数吗？

设计意图：作为高中必修一的第一章，让学生产生初高中认知的联系，并给出一个用初中函数定义无法解决的问题，激发学生的兴趣去探究新的函数定义。

2.函数的单调性

引例：画出并观察下列三个函数的图像，说出其图像变化趋势。

y=2x，y=−2x，y=x2

设计意图：利用数形结合的数学思想，结合初中关于一次函数y=kx+b（k，b为常数，且k≠0）的性质：当k>0时，y的值随x的值增大而增大；当k<0时，y的值随x的值增大而减小；以及一元二次函数的图像变化趋势让学生更加直观地体会增减性，教师通过了解到学生的认知变化，有效地进行知识的传递。