基于深度学习的高中数学教学设计

虽然觉知还不是深度学习的真正领域，但它为深度学习做好了心理上的准备。接下来，深度学习就自然要进入分析、综合阶段，在这一阶段，学生从整体到部分和部分到整体的角度认识新知识，并对新知识进行整合和意义建构。为了使学生更好地理解知识、建构知识，教师可以采取以下教学策略。

（一）注重合作，建立学习共同体

在学习过程中，教师有必要引导学生建立学习共同体，在小组学习中进行合作，因为在“学习共同体”中，学生的互动活动会促进他们的认知活动。在教师下达学习任务时，学生会在任务中思考问题，通过讨论和交流形成自己的判断，表达自己对问题的理解和解决问题的不同想法。学生在互动的过程中分享了自己的观点，扩大了自己的知识^[3]。

（二）引导学生运用多种方法实现知识的意义建构

“我常常在课堂上边听边思考，努力理解新的知识”一题的调查结果显示大多数学生能够做到理解性的学习知识。作为教师，为了使学生更好地理解新知识，并实现新知识的意义建构，可以引导学生运用多种方法，包括实验、类比推理、归纳推理和从特殊到一般，等等。

1.运用操作实验

直接经验对学习数学具有特殊意义，条件允许的情况下，让每一位学生动手参与数学实验是他们实现意义构建知识的有效学习方式。如在“指数函数的性质”教学时，可借助几何画板让学生进行数学实验，学生通过随意取值画出相应的指数函数图像，观察、讨论交流底数对指数函数的性质的影响。然后动态演示函数图像的变化情况，让学生更为直观地感知指数函数所具有的一般性质。在函数图像的变化实验中，诱发学生的思维冲突，使学生主动调整对指数函数的认知，在经历师生讨论、交流和逐步分析后，归纳出指数函数的性质，最终达到对指数函数的性质的有效意义建构。

2.运用类比推理

类比推理活动是实现意义建构的重要方式。在进行类比推理活动时，首先要引导学生在原有的认知结构中寻找恰当的类比原型；其次，根据类比原型的结论及其推导的方法，提出类比猜想，再进行检验或证明。如在“等比数列的性质”教学中，引导学生从等差数列的性质入手，运用类比推理得到等比数列的性质。

师：根据前面学习的知识，我们知道在等差数列{an}中，若自然数m，n，p，q满足：m+n=p+q，则am+an=ap+aq。那么在等比数列中有没有类似的结论呢？

生1：在等比数列{an}中，自然数m，n，p，q满足m+n=p+q，则am+an=ap+aq。(www.xing528.com)

生2：在等比数列{an}中，自然数m，n，p，q满足m+n=p+q，则aman=apaq。

师：两位同学的猜想哪一个正确呢？（学生动手证明两种猜想）

生：运用等比数列的通项公式可以证明第二种猜想正确。

3.运用归纳推理

归纳推理是对同类事物中所蕴含的同一性或相似性而得出此类事物的一般性结论的思维过程，它也是实现知识意义建构的重要方式。如在“同角三角函数的基本关系式”教学中，教师可以引导学生计算下列各式的值：sin230°+cos230°；sin245°+cos245°；sin260°+cos260°，通过运算，发现各式的值均为1。

师：这一结论能否推广到任意角a，猜想有什么结论？

生：sin2a+cos2a=1。

师：很好。又由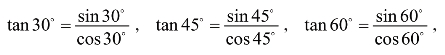推广到任意角，猜想有什么结论？

生：

师：如何证明这些公式？（引导学生联想三角函数的定义）