清史学者汪莱的贡献与研究

《清儒学案》卷一百二十六《四香学案·四香交游·汪先生莱》：汪莱，字孝婴，号衡斋，歙县人。年少补诸生，力学，通经史及推步历算之学。嘉庆戊辰优贡生，充八旗官学教习。国史馆续修《天文》、《时宪》二志，举先生与徐准宜、许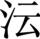充纂修官。书成，授石埭训导。先生与四香同治李冶、秦九韶之学。……所著有《衡斋算学》七卷、《考定通艺录磬氏倨句解》、《参两算术》、《十三经注疏正误》、《说文声类声谱》、《今有录》、《衡斋诗文集》。(参史传、《续畴人传》、焦循撰《别传》、胡培翚撰《行略》)

《清史稿·畴人二》：汪莱，字孝婴，号衡斋，歙县人。年十五，补博士弟子。弱冠后，读书于吴葑门外，慕其乡江文学永、戴庶常震、金殿撰榜、程征君易畴学，力通经史百家及推步历算之术。嘉庆十二年，以优贡生入都，考取八旗官学教习，会御史徐国楠奏请续修《天文》、《时宪》二志，经大学士首举莱与徐准宜、许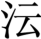入馆纂修。十四年，书成。议叙，以本班教职用，选授石埭县训导。十八年，应省试，得疾归，卒于官，年四十有六。先是十一年夏，黄河启放王营减坝，正溜直注张家河，会六塘河归海。两江督臣奉上命，查量云梯关外旧海口与六塘河新海口地势高下，延莱测算，盖其精算之名，久为官卿所知。曾制浑天、简平、一方各仪器观测。与郡人巴树谷最友善，客江、淮间，又与焦孝廉循、江上舍藩、李秀才锐，辩论宋秦九韶、元李冶立天元^[1]一及正、负开方诸法。天性敏绝，极能攻坚，不肯苟于著述。凡所言，皆人所未言，与夫人所不能言。尝以古书八线之制，终于三分取一，用益实归除法求之，其一表之真数，仅得十之二。因悟得五分之一通弦与五分之三通弦交错为三角形，比例立法，以取五分之一之通弦，而弦切之数益密。梅氏环中黍尺，有以量代算之术，惟求倚平仪外周之两角，而缩余内半周之角未详。其法较易，因立新术，量取不倚外周之角度，而三角之量法乃全。堆垛有求平三角、立三角、尖堆积法，不及三乘方以上，又复推而广之，自三乘、四乘以上之尖堆，皆可由根知积。并及诸物递兼之法，以补古《九章》所未备。又纠正梅文穆公句股知积术，及指识天元一，正、负开方之可知、不可知。其纠正句股知积术也，文穆《赤水遗珍》称：“有句股积及股弦和较求句股，向无其术，苦思力索，立法四条。”其门人丁维烈又造减纵翻积开三乘方法，文穆许之。莱谓：“句股形等积、等弦和，带纵立方形等基、等高阔和，皆有两形互易。如句二十，股二十一，弦二十九，句弦和四十九，句股积二百一十。若句十二，股三十五，弦三十七，句弦积亦四十九，句股积亦二百一十。设问者暗执一形，则对者交盲两数。梅、丁诸公法成而不可用，盖两句弦较，与一句弦和，恒为连比例之三率。其两句弦较，即首、末二率；两较减一和之余，即中率；而句弦和必为三率并。遂创立有两积相等、两句弦和相等、求两句股形之法。以四倍句股积自乘，句弦和除之，为带纵长立方积。以句弦和为纵，开得数为两句弦较之中率，自乘为带纵平方积。又以中率与句弦和相减为长阔和，求得长阔两根为两句股较，用求两句股形各数。又同积之边，彼此可互，三次之乘，先后可通，故四倍句股积自乘，即两形之倍句相乘为底，两形之股相乘为高，即犹以中末乘首。中化为中率，再乘为立方三率，并为带纵。由是推得立方形两高数恒为首末二率，高阔和恒为三率，并数与等积、等弦和之两弦较及弦和丝毫无异。如高九阔十，高阔和十九，立方积九百。若高四阔十五，高阔和亦十九，立方积亦九百，其数莫不由两形相引而出。故其法即命积为带纵长立方积，以高阔和为所带之纵。用带纵长立方法开得本方根，为两形高数之中率。与高阔和相减，余为带纵之平方长阔和。中率自乘，为带纵平方积。用带纵平方长阔和法开之，得长阔一根，为两形之两高数。两高与和相减，为两阔数。”其指识正、负开方也。“元李冶传洞渊九容术，撰《测圆海镜》、《益古演段》，以明天元如积相消，其究必用正、负开方，互详于宋秦九韶《数学九章》。梅文穆公虽指天元一为西人借根方所由来，而正、负开方则未有阐明者。元和李秀才锐特为雠校，谓少广一章，得此始贯余一。好古之士，翕然相从。莱独推其有可知、有不可知。如《测圆海镜》边股第五问‘圆田求径二百四十步与五百七十六步共数’，而李仁卿专以二百四十为答。《数学九章》田域第二题‘尖田求积二百四十步与八百四十步共数’，而秦道古专以八百四十为答。乃自二乘方以下，缕析推之，得九十五条。凡几根数为带纵长阔较则可知，为带纵长阔和则不可知。又推得几真数少，几根数又多，几平方与一立方积等多少杂糅，和较莫定。立法以审之，以几平方数用几立方数除之，得数乘几根数，以较几真数。若少余真数，则以几平方为高阔较，是为可知。若多余真数，则或几平方为通分法，三母总数、几真数为三母维乘之共数，几根数为通分之共子，如二、如六、如十二。设真数一百四十四，少二百八，根数多二十，平方积与一立方积相等，则三数皆同，是为不可知。”盖以一答为可知，不止一答为不可知。故李秀才锐跋其书，括为三例以证明之。谓：“隅实同名者不可知；隅实异名，而从廉正负不杂者可知；隅实异名，而从廉正负相杂，其从翻而与隅同名者可知，否则不可知。隅实异名，即带纵之长阔较也，较仅一答；隅实同名，即带纵之长阔和也，和则不止一答。”锐以隅实同名、异名，明一答与不止一答；莱以长阔、和较，明可知、不可知，其义一也。著有《衡斋算学》七册、《考定通艺录磬氏倨句解》一册。

《清史列传·儒林传下二》：存目。^[2]

焦循《雕菰集》卷二十一《石埭儒学教谕汪君孝婴别传》：吾友汪君孝婴，嘉庆丁卯以优贡生赴朝考京师。戊辰入国史馆，纂修《天文》、《时宪志》，既成，天子嘉其通晓数学，授教谕，选石埭儒学教谕。癸酉冬十一月，卒于官。明年甲戌冬十二月，其弟子绩溪县举人胡君培翚移书于循，曰：“国史馆修《儒林传》，馆内诸公征先师事迹，窃思先师六经、子、史罔不通贯，而天文、算术是其专门，非得精通九数者不能道，且先师所学与自来各家异同出入，未易悉其涂径，伏唯先生于数学著有成书，先师寓扬时惟与先生往来商榷，倘不吝惠施，俯从所请，为撰《别传》一篇，将先师心得详悉揭出，以便上之史馆，感且不朽。”呜乎，孝婴信没矣！自丁卯与孝婴别去，秋省试后，孝婴与舍弟同舟至扬，信宿遽去，循村民，以足疾未获一晤。近者传闻其没，犹未敢信，得胡君书，而孝婴信没矣。孝婴少余五岁，自订交于秦淮旅舍，至今二十余年，虽远隔数千里，有所得，必邮寄，相与论订。岁丙寅，余馆城中，与孝婴馆相去数武，尤朝夕聚。然孝婴之学深妙入微，恐不足以尽其蕴，姑述所知，质之胡君，惟大人先生采摘焉。孝婴姓汪氏，讳莱，号衡斋，徽州歙县人也。徽州之学，自江文学永倡其先，戴庶常震、金殿撰榜、程孝廉方正瑶田踵而兴焉。江氏精西人法，戴氏饰以古九章割圆，故天文术算与宣城梅氏相伯仲。东吴钱少詹事大昕、教授塘遥相应和。然孝婴生于歙，其学实自得，不由师授，弱冠后读书于吴葑门外，数年苦心冥索，尽得中西之秘，亦未尝与吴中师友相接，天资敏绝，性能攻坚，极繁赜幽秘，他人翻覆再三未能理其绪，而孝婴目一二过，默识静会，已洞悉其本原，而贯达其条目，是非间隙，豪发莫遁。人所言不复言，所言皆人所未言与人所不能言，故其著述无多卷，而简奥似周、秦古书。八钱之制，终于三分取一用，益实归除法求之，孝婴以一表之真数仅得十之二，因悟得五分之一通弦与五分之三通弦交错为三角形，比例立法，以取五分之一之通弦，而弦切之数益密。梅氏《环中黍尺》有以量代算之术，惟求倚平仪外周之两角，而缩于内半周之角未详。孝婴以为易，更立新法量取，不倚外周之角度，而三角之量法乃全。堆垛有求平三角、立三角、尖堆积法，不及三乘方以上，孝婴推而补之，自三乘、四乘以上之尖堆，皆可由根知积，因及诸物递兼之法，以补《古九章》所未备。凡此引伸触类，无不探幽索隐，条疏层解，所尤独得者，为纠正梅文穆公句股知积之术，及指识天元一、正负开方之可知不可知。文穆《赤水遗珍》称“有句股积及股弦和，较求句股”，向无其法，苦思力索，立法四条。其门生丁维烈又造减从翻积开三乘方法，文穆许之。孝婴曰：“句股形等积等弦和，带从立方形等积等高阔和，皆有两形互易，如句二十、股二十一、弦二十九，句弦和四十九，句股积二百一十；句十二，股三十五，弦三十七，句弦和亦四十九，句股积亦二百一十。若问者暗执一形，则对者交盲两数，梅、丁诸公法成而不可用。”遂创立有两积相等、两句弦和相等求两句股形之法。其法四倍句股积自乘，句股和除之，为带从长立方积，以句弦和为从，开得数为两句弦较之中率，自乘为滞从平方积，又以中率与句弦和相减为长阔和，求得长阔两根，为两句弦较，用句弦较与句股和，求得两句股形各数。盖悟得两句弦较及两句弦较减一句弦和之余，必为连比例之三率，两句弦较必为首末二率，两较减一和之余必为中率，句弦和必为三率并，故求得首末两率，即得两句弦较之数。又悟得同积之边彼此可互三次之乘，先后可通，故四倍句股积自乘即两形之倍句，相乘为底，两形之股相乘为高，又以股自乘，同于句弦和乘句弦较，则以句弦和除股自乘原可得句弦较。今之两倍句不同数，和乘之两股亦不同数，则句弦和乘之不得句弦较，而得两句弦较之中率。盖句弦和既为三率并，则此一句弦较为首率者，用减此一句弦和，所余倍句即中末二率，彼一句弦较为末率者，用减彼一句弦和，所余倍句即首中二率，故两倍句相乘，即犹以中末乘首中，而两倍句相乘为底，两股相乘为高者，化为中率。再乘为立方三率并为带从。故以句弦和为从，开立方即得中率，又以中率自乘，与首末二率相乘等。故以中率自乘为平方积，以首末二率为长阔和，得长阔即得首末，得首末即得两句弦较之数。是术也，穷消息之原，凿旁通之径，所谓成变化而行鬼神者矣。元李冶传洞渊、九容之术，撰《测圆海镜》、《益古演段》，以明天元一。如积相消，其究必用正负开方，互详于宋秦九韶《数学九章》。本朝梅文穆公虽指天元一为西人借根所由来，而正负开方则未有阐明者。元和李锐尚之特为雠校，谓少广一章得此始贯于一，好古之士翕然相从。孝婴独推其有可知有不可知，如《测圆海镜》边股第五问，圆城求径二百四十步与五百七十六步共数，而李仁卿专以二百四十为答；《数学九章》田域第二题，尖田求积二百四十步与八百四十步共数，而秦道古专以八百四十为答。乃自二乘方以下，缕析推之，得九十五条，凡几根数为带从长阔较则可知，为带从长阔和则不可知。又推得几真数少几根数又多几平方与一立方积等，多少糅杂，和较莫定，立法以审之，以几平方数用几立方数除之得数乘几根数，以较几真数。若少于真数，则以几平方为高阔较，是为可知，若多于真数，则或几平方数，为通分法三母总数，几真数为三母维乘之共数，几根数为通分之共子。如二如六如十二，设真数一百四十四，少二百零八根积多二十平方积与一立方积相等，则三数皆同，是为不可知也。孝婴于六经务在熟习本文，博通注疏，原始要终，以一知半解为陋。(下略)

胡培翚《研六室文抄》卷九《石埭训导汪先生行略》：培翚年二十余，始知厉学，广求师友，见有方正博闻之士，必就咨访。一日，遇先生于郡学署，先生之名所素仰也，时方读《周礼疏》，即举所疑以问先生，为言郑注若何，贾疏若何，不惟详其义，并诵其辞。私以为偶熟是条，耳及数问，皆然悚然起敬，遂介郡学夏师受业焉。故先生之行谊颇闻其略。先生姓汪氏，讳莱，字孝婴，号衡斋，歙之瞻淇人。父讳昌，乾隆乙酉举人，著有《静山堂诗稿》。先生七岁能诗，十五补博士弟子，力学通经史百家，精推步布算之术，制浑天简平一方，各仪器观测，与郡人巴孟嘉氏切磋友善。年三十余，客江淮间，又与焦君里堂、江君郑堂、李君尚之论算法，诸君皆折服。同邑程征君易畴尝以磬折古义属考定焉。嘉庆十年，郡学司训夏师高其学，与教授朱师同举先生优行督学，今尚书周连堂先生试经解、诗赋、时艺，俱冠其军，遂食廪饩。继任督学今侍郎戴紫垣先生与署巡抚鄂公会考，丁卯优行，以第一贡成均。先是十一年夏，黄河启放王营减坝正溜直注张家河，会六塘河归海，两江总制铁公奉上命，查量云梯关外旧海口与六塘河新海口地势高低，实延先生测算，盖先生精算术，为公卿所知久矣。本朝《天文》、《时宪》二《志》自雍正十三年后久未修辑，嘉庆十二年御史徐国楠奏请续修，经大学士等议准移付史馆，史馆向例以翰林中书为纂修、协修等官，于是总裁传问诸翰林中书官无有通晓天文者，会先生十三年入都朝考，兼考取八旗官学教习，大学士庆公等即首举先生与徐准宜、许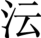入馆纂辑，奉旨允准。然二志实皆先生一手纂办。十四年书成，议叙各以本班尽先选用，而先生得石埭县训导。十五年春莅任，悉心教士以穷经力行为先务，邑人自是咸知向学。石埭文庙向未具乐器，先生倡议捐俸制办修造乐舞等器，共一十七宗一百五十八件，质文度数悉遵《御制律吕正义》，成式无分寸之逾，司乐生二十人，舞生四十人，先生与之朝夕讲肄，弦歌舞蹈，悉遵钦颁乐章字谱，无纤悉之讹。池郡守何公为撰文纪其事，树石明伦堂。十八年应江南乡试，得疾回署，遂以是年十一月二十日卒。生于乾隆三十三年七月初七日，年四十六。子二：长光恒，时才四岁；次光谦，未周月。先生廉介自持，一毫不苟取。卒之日，囊橐萧然。石埭士民咸感伤，相约醵金赙助，送其家，扶^[3]归歙。先生读书具深识，过目辄记，然不肯苟于著述，以为必有关绝续之大，能发千古之疑，始立言以传后。所著有《衡斋算学》七册……先生之学大略有三，曰算学，曰经学，曰小学。算学自弱冠后馆吴中三年归学成，著书刊布，艺林海内通人言天文、算术必推先生，其精妙入微，发前人所未发，焦君里堂作先生《别传》，详哉其言之矣。《别传》附刻于后。至经学、小学之书，既未传世，知之者少，然生平用力实深。诸经注疏皆能成诵，贯串在胸，是非得失无不了彻。汉、唐诸儒疑谬相承之说，一经勘正，涣然冰释。……深于郑氏一家之学，尝曰：“郑氏《三礼注》，一义必通贯全书，一文必准称千古。”诚笃论也。又曰：“郑氏《易注》以象为主，先取本卦之象，无则取之卦之象、互卦之象，之而互之，象爻辰上值列宿之象，令圣人系辞无一字虚设，较王辅嗣之宗尚玄虚诚为得已，然犹有议者。夫子言彖者言乎象，爻者言乎变，是解彖辞不应取之卦之象，解爻辞惟当取一爻独变之象，康成注按之此例，尚未悉协。”因欲综全经，作《易疏》，未就。经学之书，成者惟《十三经注疏正误》，遗本今存及门汪孝廉延麟处。熟于字书，有问奇者，随举无毫发爽。尝撰《说文声类》，以篆手写定本，藏于家。自序谓始嘉庆戊午，迄辛酉，三阅寒暑，乃克卒业。夫古人文字起于声音，有声而后有字。《说文》之某声实六书枢纽，特许氏本书以偏旁分别部居，读者罕得其条理。先生取某声及读若之声研贯钩比，类次成帙，而六书之本旨以明。又作《声谱》，明切韵之学，开合俱分土、金、木、火、水，五宫用平、上、去，而无入声，著《三声论》，辨入声为上浊，其言曰：声止于三，一曰平，二曰上，三曰去，三声皆有浊声，而上声之浊最显。定声类者不审其精读之过急，乃于清声之后，继以上声之浊，而别之为入声，相沿至今，习焉不察，韵书葛藤从此起已，故有以去浊为上入之浊者，等韵群、定诸母是也。说者谓上声之浊似去而非去，今观群、定诸母则诚然矣，疑、泥诸母何以又不似去乎?盖既误别上浊为入声，因求群、定之声而不得，遂取方音别上入字之讹为去浊者而填之，以声而论，则真去也何似之有?至疑、泥诸母既因平声之清无字不立其母，又遂竟以清声填诸浊位，此误别入声，致生支离之咎也。有上、入不分清浊二位，任意通用者，《经世音图》暨《韵法直图》是也。盖欲于上、入之外别其清浊，而不能别因重其声以拟平、去，而不可分此，误别入声，致生蒙混之咎也。有制啌、嘡、上、去、入为五声，而上、去、入皆不分清浊者，方以智之《通雅》是也。盖既误上浊为入声，别求上入之浊而不得，遂疑仄声一例并去浊而昧之，此又误别入声，致生挂漏之咎也(汪士铎谨案：古无入声之说，孔巽轩亦详言之。或以此论为可删，未然其言)。穷流溯源，洞见韵书疵颣，先生经学、小学之大略粗存于此矣。天性孝友，少时贫困，竭力养亲，恒负米数十里外，尝典衣，为犬啮，秘不令亲知，值岁歉，不能营二鬴，百计谋甘旨以奉二人，自乃从山氓采石面充腹，喉格格不能下，强咽之，肠为之塞，退而形诸歌，咏以自叹，厚族党，雍睦无闲言，与人交，和而介，待问勤恳不倦，往复论晓，必令问者释然乃止。培翚自丙寅冬执弟子礼，未几，而先生入都，嗣后南辕北辙，动辄相左，中惟己巳归里，得一再奉教，吁可伤已！去冬过邗江，既以其学之大者，丐焦君作传，兹与先生甥洪铎料理遗书，益增感怆。恐先生行迹日就湮没，乃谨以所闻知叙次于右。嘉庆二十年乙亥九月，胡培翚谨撰。

江藩《国朝汉学师承记》卷六有传，存目。(www.xing528.com)

【注释】

[1]天元：算法名。本古代九章方程，相当于今代数中的一元方程式。宋秦九韶《数书九章》、元李治《测圆海镜》、《益古演段》、朱世杰《四元玉鉴》都运用了这种算法。

[2]见中华书局本第18册，第5591～5592页。

[3]：载运棺柩的车。《释名·释丧制》：“舆棺之车曰。，耳也，县于左右前后铜鱼摇绞之属。”《文选·潘岳〈寡妇赋〉》：“龙俨其星驾兮，飞旐翩以启路。”李善注：“，《说文》：‘丧车也。’”