八卦模型：复合命题的重大作用

古老的文化，往往笼罩着神秘的色彩，太极八卦便是一例。八卦源于我国，相传为上古圣人伏羲氏所创。由于它结构奇特，使人有变幻莫测之感，因此古人把它用作占卜，图谶问卦，宣扬“天命”，使之又蒙上了一重迷信的烟尘。

古人认为阴阳二气是宇宙之本，所以太极八卦图的正中央画的是一对头尾相咬的阴阳鱼，周围是八组不同的“三线图”，由阴阳符号组成，阴缺阳实：

如果把八卦图中的“—”译为“1”，而把“ ”译为“0”，那么八卦的三线图便与二进制数建立以下对应关系：

由此可见，八卦实际上是最早的二进位制。在欧洲，二进制的建立始于德国数学家莱布尼兹（公元1703年）。莱布尼兹自认他的发现是受伏羲氏所创八卦的启发。

上表的最右一列，是将八卦符号改写为立体坐标的形式。有趣的是：表中八个坐标代表的点，恰好构成空间单位正方体的八个顶点。读者很快就会看到，这种相当直观的立体八卦模型，在我们复合命题的简化中，将起着何等重大的作用！

上一节我们看到，许多表示复合命题的逻辑式，是由基本命题及其否定之积相加的形式表现出来。这样的式子称为逻辑和的标准形式。例如：

等等。最后一个逻辑式，它的每一项积包含有全部的基本命题或其否定。这样的逻辑和标准形式称为“完全的”。

很明显，一个非常标准形式的逻辑式，可以通过展开化为标准形式。而一个标准形式的逻辑式，又可以进一步化为完全标准形式。这只需反复应用X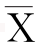＋＝1这一公式即可。例如：

读者完全可以想象得到，一个复合命题的“完全式”，可以在前面提到的立体八卦模型上表示出来，只是把三条坐标轴换成基本命题A、B、C罢了。这样，“完全式”的某个顶，便表示为下图立方体中的某个顶点。标出这些顶点，便得到相应复合命题的几何模型。

例如，对于复合命题

我们可以分别得到如下的几何模型：（见下图）(www.xing528.com)

可能读者已经发现，图中的某些棱已被画为粗线。这是因为当一条棱的两端同时出现在逻辑和表示式中时，该逻辑式一定可以简化。例如左下图的点（）与（ABC），由于

这意味着它可简化为连接两点的棱BC。由图知，X、Y可简化为：

同理，若立体模型中某个面的四个顶点同时出现在逻辑和表示式中，那么这部分的表示式便可简化为代表这个面的一个字母。例如，前面提到的右端四项，分别表示上图A面上的四个顶点，于是T可简化为A。事实上，直接计算有：

需要说明的是：在作命题简化的时候，我们只需从逻辑和的标准式开始就可以了。因为标准式一般比“完全式”来得简单。引进“完全式”只是为了讲解上的方便。实践上对于已经简化了的东西，是无需回到更为复杂的模式上去的。这好比马拉松赛跑，此时你已经跑了三千米，如果你想向观众表明你有能力跑完全程，那么你完全不必回到起点去重新跑起，接下去跑到终点就是了！

为了让读者有所仿效，下面我们举一个用立方简化复合命题的完整的例。已知：

画出命题U的几何模型容易看出，图中有四个顶点位于A面上，从而命题U可以简化为：

U＝A＋BC

可能有的读者会问：前面讲的都是三个基本命题的情形，对于四个或更多基本命题的情形又该怎么办呢？要回答这个问题我们还需要许多其他的知识，例如需要了解四维立方体或多维立方体的概念等等。由于哪怕只做最粗略地介绍，也要花费巨大的篇幅，因此我们除提一提四维空间之外，其余便从略了！

提到第四维，读者可能感有点神秘，其实我们生活着的时空便是四维空间，时间就是第四维，世间的万物全都在时间的长河里流淌！我们只有用时间和空间，才能准确地描绘我们周围发生的事件。如果我们把龙年除夕之夜的地球轨道看成一个平面，而我们又有一个硕大无比的立方体绕着太阳在同一平面上运转，那么时间作为第四维的意义，将更加直观地显现出来。

至于四维立方体，可以想象成一个普通的立方体，随时间推移而逐渐缩小，过单位时间之后，定格为内部的小立方体，如同左图所示。这可是一个奇怪而有趣的图形哩！它有16个顶点，24个面和32条棱！至于如何利用它去简化含有四个基本命题的复合命题，就留给读者去思考了。不过，千万别小看这，它可得费一番脑筋呢！