衍生品定价：风险溢酬的估计

通读经典金融文献可以发现，金融学者们研究风险溢酬不外乎两大思路：一是用期权和其标的资产的信息进行联合估计，从期权价格中估计出风险中性测度下的期望值，从标的资产价格中估计出现实测度下的期望值，而后运用测度转换的基本思路，得到相应隐含的风险溢酬；二是仅从标的资产价格信息入手，用标的资产（如个股）构建风险因子，用FM两步法进行回归，估计相应的风险溢酬。那么，同样是研究风险溢酬，这两种方法之间是否存在一定的联系呢？迄今为止，尚无学者清晰地论证过这两种方法之间的联系与差异。在这一部分，我们将借助随机贴现因子的分析框架就这个问题进行讨论，证明这两种方法的内在一致性，也相应证明了本章接下来通过标的资产价格进行的跳跃风险溢酬的研究结论是稳健的，与通过期权价格研究跳跃风险溢酬得到的结论在理论上是一致的。

我们首先从经典的FM两步法开始分析。假设只有单个风险因子F。FM两步法主要基于APT模型（arbitrage pricing theory，又常被称为因子模型），第一步首先对标的资产（通常为个股）收益率R i与风险因子F进行时间序列回归，即

得到个股i对风险因子F的因子载荷，即系数βi，F，视为个股i收益率对风险因子F的敏感性，αi和ζi，t分别为截距项和残差项。第二步，用下一期个股的超额收益率对个股的βi，F进行横截面回归

其中R f为无风险利率，μ和ηi分别为截距项和残差项，最终估计得到的系数λF就是风险因子F的单位风险溢酬（也被称为风险价格）：对于i股票来说，每单位风险溢酬λF乘以该股票对F风险的敏感度βi，F，显然就是投资该股票、承担来自F的风险而应获得的总风险溢酬。如果λF显著异于零，说明风险因子F被定价；反之则未被定价。

下面我们在随机贴现因子的分析框架下对FM两步法进行更深入的分析。对于任意资产i的收益率R i，根据随机贴现因子（stochastic discount factor，SDF）的基本原理[2]，我们有：

其中m表示随机贴现因子[3]，而且m和R i所对应的期间是相同的。略加推导可以得到

为了展开cov[R i，m]，可以将m与F的关系写为

其中，回归系数b的公式为

ε中则包含了因子F之外的其他定价因子。

这样，式（6.4）可以继续写为

对比式（6.1）、式（6.2）与式（6.7）可以看出，式（6.7）中的就是时间序列回归式（6.1）中得到的βi，F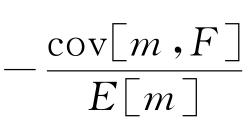，就是横截面回归（6.2）中的单位风险溢酬λF。因此，式（6.1）和式（6.2）实际就是式（6.7）的计量表达式，ζi，t则反映了其他定价因子对R i的影响。(www.xing528.com)

进一步分析单位风险溢酬

其中m和F的协方差可以分解为

其中E[·]表示现实测度下的期望值。根据随机贴现因子的基本原理可知，

其中表示风险中性测度下的期望值。由于随机贴现因子具有性质

式（6.9）可以进一步写成

将式（6.12）代回单位风险溢酬的表达式（6.8），可以看到这两个式子是等价的。即

式（6.13）向我们揭示了一个非常重要的结论：现实测度下与风险中性测度下风险因子F的期望值之差就等于F的单位风险溢酬。换言之，运用FM两步法从标的资产价格信息中估计得到的风险溢酬与运用测度转换从期权价格信息中得到的风险溢酬是等价的[4]。具体到本章，可以得出的结论就是：运用FM两步法、采用股票数据，可以在缺乏期权市场的情形下，向我们提供中国市场跳跃风险和跳跃风险溢酬的信息，进而预先对未来中国金融市场上的期权受模型风险的影响提供参考。

在下文中，本章将按照FM两步法的基本流程——式（6.1）和式（6.2）——进行研究。从两个回归式中可以看出，要进行FM研究，需要输入跳跃因子的时间序列，因此我们要先侦测出中国市场上的跳跃现象，然后采用Fama-French方法，用可交易模拟组合（mimicking portfolio）的收益率来代表跳跃因子估计出因子载荷，再进行跳跃风险溢酬的估计。

需要强调的是，只有在FM两步法采用单因子模型时，我们才有式（6.13）。原因有两点：第一，在前面的推导中，用随机贴现因子将风险溢酬与实证研究相结合时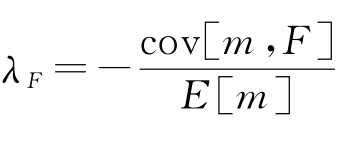，的结论是在单因子框架下才能够得出的。第二，在期权定价模型中，风险源往往只来源于跳跃风险以及扩散风险，从而期权定价中的风险溢酬也同样只分为扩散部分所带来的风险溢酬以及跳跃部分所带来的风险溢酬。而在因子模型中，我们可以很简单地加入多因子，但多个风险因子往往无法在期权定价模型中以风险源的形式全部体现出来，从而会失去一一对应的性质。例如，在多因子模型中得到的规模因子风险溢酬、流动性风险溢酬等等可能体现在期权定价模型中的跳跃幅度风险溢酬或者跳跃频率风险溢酬中。基于这个考虑，下文中为了检验已有研究（如Pan（2002）[47]；Eraker（2004）[35]和Broadie，Chernov and Johannes（2007）[48]）对三个维度的跳跃风险溢酬设定的正确性，本章将先检验单因子模型，来检验在中国市场这三个维度的跳跃风险是否都需要风险溢酬。之后，依据传统的因子回归的方法，也进行多因子回归，但加入其他因子的主要目的是引入控制变量来探讨跳跃风险因子是否能够被其他因子所解释。