跳跃风险因子统计及构造

由于本章研究的重点是SPX期权中所隐含的跳跃风险、跳跃风险溢酬以及它们对复制误差的影响，因此在实证方程（5.1）的右边，我们最关注的就是跳跃风险因子的代理变量Jump应如何选取。在以往的研究中，学者们尝试过的跳跃风险代理变量包括：期权中隐含的标的资产收益率的偏度、峰度Bakshi and Kapadia（2003）[59]、短期期权的隐含波动率曲线在平价附近的斜率（Yan（2011）[50]）等。Bakshi and Kapadia（2003）[59]发现在模型中加入跳跃风险，会使得期权的隐含偏度和隐含峰度发生变化。但期权的隐含偏度、隐含峰度与隐含波动率仍然有着密不可分的联系。原因是，偏度和方差的协方差Cov（skewness，variance）实际上是五阶矩，而偏度和方差的协方差Cov（kurtosis，variance）则是六阶矩。因此，当更高阶矩，比如五阶矩和六阶矩不为零时，期权的隐含偏度和峰度信息中很可能包含大量的二阶矩信息，不一定完全代表跳跃的信息，将其作为代理变量并不十分完美。而Yan（2011）[50]则证明了在短期内，期权的隐含波动率曲线在平价附近的斜率满足以下表达式

其中，IV为期权隐含波动率（implied volatility），Moneyness的计算公式为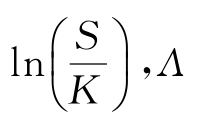是跳跃的密度，而J是跳跃的幅度，σ为瞬时波动率，Ο（TTM）代表与剩余期限同阶的数值。

式（5.1）表明，只要选择剩余期限较短[6]、接近平价的期权，Ο（TTM）就是一个较小的数，而期权隐含波动率和资产价格的跳跃之间就存在非常密切的关系。在式（5.1）的基础上，Yan（2011）[50]进一步得到了一个更加易得的跳跃风险代理变量

其中，分别表示剩余期限相同，Delta＝－0.5的看跌期权与Delta＝0.5的看涨期权的隐含波动率，a是一个大于零的常数。

式（5.2）意味着，之差约等于跳跃概率与跳跃幅度的乘积再乘以一个常数。可以看到，和之前的偏度等指标相比，式（5.2）的指标更加干净，它基本上只包含了跳跃的相关信息。基于此，本章最终选定采用Yan（2011）[50]的方法，即式（5.2）来构造跳跃风险因子的代理变量Jump。图5.3给出了跳跃风险因子在样本内的表现。

图5.3　跳跃风险因子在样本期内的历史走势

从图5.3可以看出，无论是在2001年的互联网泡沫崩溃期间，还是在2008—2009年的次贷危机期间，我们构造的跳跃风险因子都曾出现极端的“黑天鹅”事件——巨幅的向下跳跃，次贷危机下的极端情形显然更为严重。这初步验证了我们所构造的跳跃风险因子的合理性。表5.2进一步报告了跳跃风险因子在全样本和两个子样本期间的描述统计。

表5.2　跳跃风险因子的描述统计(www.xing528.com)

从表5.2可以看出，在不同样本期中，跳跃风险因子的统计特征有所差异。在子样本1中，跳跃风险因子的均值与中位数均为正，这显然是因为互联网泡沫崩溃期较短，2008年3月之前，整体而言跳跃为正；到了子样本2中，次贷危机和欧债危机接踵而至，大幅下跳频发，导致跳跃均值为负，这反映了危机期间期权市场隐含着对未来资产价格走势的极端负面预期；在全样本中，受子样本2中的大幅下跳影响，跳跃的平均方向是向下的。

由于跳跃风险是本章关注的焦点，在进行实证研究之前，我们希望对跳跃风险的这一代理变量进行更为深入的考察，希望了解跳跃风险因子后面的影响因素。从经济理论上看，信息冲击和流动性冲击等等最有可能是跳跃产生的原因，一般认为，平均交易量和买卖价差可以视作上述两个因素的代理变量。因此，我们的基本想法是将跳跃风险因子Jump对计算Delta＝－0.5的看跌期权与Delta＝0.5的看涨期权的平均交易量Vm和买卖价差Spd进行回归，考察它们之间的关系。同时，由于在Yan（2011）[51]的方法下，跳跃风险因子是一个近似的代理变量，而且该因子只有用短期期权进行构造才较为准确，为了避免跳跃因子构建误差的影响，我们在回归中加入Delta＝－0.5的看跌期权与Delta＝0.5的看涨期权的平均隐含波动率AIV、平均隐含波动率的倒数（控制非线性）及其剩余期限TM[7]作为控制变量[8]，从而设定回归方程为

表5.3报告了回归的结果。

表5.3　跳跃风险因子的影响因素

注：括号中为t值，∗、∗∗和∗∗∗分别表示10％、5％和1％的显著性水平。

从表5.3报告的结果中，我们发现一个非常有趣的现象：不同子样本的估计结果差异巨大。例如，截距项和三个控制变量的系数符号都是相反的，且大部分是显著的。这与跳跃方向密切相关。正如表5.2所示，在子样本1中，跳跃风险因子的均值是正的，而在子样本2中，跳跃风险因子的均值却是负的。因此，可以认为，三个控制变量对跳跃风险因子绝对值的影响都是同向的。另外，期权剩余期限在子样本1中对跳跃风险因子有影响而在子样本2中没有影响，这表明Yan（2011）[50]所建议的代理变量更适于危机期间。

在控制了上述控制变量的影响之后，我们最为关心的是期权交易量和买卖价差的显著性与经济解释。表5.3的结果表明，期权交易量无法解释跳跃风险因子，但在子样本1内，期权的平均买卖价差的系数是显著为负的，这说明在非危机期，较大的平均买卖价差是与向下跳跃联系在一起的。这是符合经济原理的：较大的买卖价差往往是市场的流动性缺失、异质信念或者投资者对未来看法的不确定性等因素导致的，这时市场往往容易出现向下跳跃。但在子样本2内，期权的平均买卖价差的系数是不显著的，这表明危机期间，期权价格隐含的跳跃风险的形成机制较为复杂。