参数复制策略：提升衍生品定价中的风险溢酬

参数复制策略的本质是用其他衍生品来对冲原先持有的衍生品对参数的一阶敏感性（Buhler and Aussprache，2005[58]）。例如，在BSM模型中，所谓对冲参数敏感性，就是用其他衍生品来对冲波动率变动的风险（即vega risk）。具体来看，参数复制策略的主要思路如下：

在任意t时刻，对于一个衍生品，用近似模型M i计算得到的模型价格与市场价格P t之间必然存在一定的误差[13]，可以表达为

也就是说，衍生品价格本来应受到标的资产价格S t和其他状态变量X t的影响。但在进行复制时，交易员只能在M i模型下进行所有的计算和操作。由于未考虑其他状态变量X t的影响，M i模型所使用的参数θt并非真实参数。用列向量表示对M i中各个参数的一阶敏感度，即

其中（·）T的上标T代表矩阵的转置。由于模型M i中包含了k个参数，因此需要k种衍生品作为复制工具来进行对冲。这k个复制衍生工具的模型价格行向量表示为

这些复制衍生工具关于模型M i参数的敏感度同样可以通过对参数求偏导得到，最终是一个k×k方阵：

其中第（p，q）个元素表示第q个参数变动一个微小的单位导致第p个衍生品的价格变动的幅度。

要使得整个组合对参数的瞬时敏感度为零，各种复制衍生工具持有量的向量显然应满足

其中

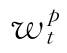，p＝1，…，k是第p个复制衍生工具在t时刻的持有量，上式经整理可得

这样，即为复制衍生工具组合在t时刻的价值。交易员持有价值为的复制衍生工具组合即可实现参数复制和风险对冲。

需要强调的是，在对冲参数风险之后，交易员还需要用标的资产对冲整个组合关于标的资产的敏感度，即再进行Delta复制策略。具体来看，为了使得整个资产组合关于标的资产的瞬时敏感度也为零，我们还必须要求在t时刻所拥有的标的资产数量满足

式（3.9）意味着，被复制衍生品对标的资产价格变动的Delta值等于整个复制工具组合（包括标的资产和其他复制衍生工具）对标的资产价格变动的Delta值。同时实现式（3.7）和式（3.9），就同时实现了复制和Delta风险对冲。(www.xing528.com)

综合（3.8）和（3.9）两式，可以发现要解出标的资产和复制工具的持有量，就是要解参数复制策略和Delta复制策略构成的方程组

这样，在每个时刻t，就可以计算出该时刻复制所需的标的资产持有量和其他复制衍生工具的持有量。注意，这两个值都是时变的，因此复制是一个不断动态调整再平衡的过程。进一步将和对t求偏导，就可以得出每个复制工具持有量的瞬时变化，即每个时刻交易员应该买卖的量。

从t 0到t时刻，将整个复制过程所需的资金贴现至t 0时刻，总现值为

注意，在上式中C t没有上标符号M i，意味着这是复制衍生工具的真实市场价格而非模型价格。而在t时刻，交易员所拥有的资产头寸总价值为

同样，上式中的资产价格都没有上标M i，代表的是真实市场价格而非模型价格。

因此，在近似模型M i下，从t 0到t时刻，总复制成本在t 0时刻的现值为

其中R为t 0到t期间的平均利率水平。相应地，用M i模型所隐含的复制策略同时进行Delta对冲和参数风险对冲的复制误差就为

从实际来看，该复制误差就是交易员交易账户的损益：初始出售衍生品的收入减去复制总成本的现值。

从理论上说，复制所需的标的资产持有量和其他复制衍生工具的持有量都是一阶导，因此复制的调整必须连续进行，在时间上无限可分。在现实中，这显然是无法实现的。在实际中，交易员的做法是将式（3.10）进行离散化，分隔成小的复制时间间隔，得到

在每个时间间隔内，标的资产与复制衍生工具的头寸分别变动和，需要融资的金额则为。再将式（3.14）代回式（3.12）和式（3.13），同样意味着我们可以从交易员账户的损益数据中估计出离散时间下参数复制加Delta复制的总误差。