衍生品定价模型的设定和误差影响

在本节中，我们将表明模型设定偏误会如何影响交易员账户的复制误差。我们以最常见的Delta复制策略为例来说明这个问题。Delta复制策略是衍生品领域最常见和最广泛采用的复制策略。因此，考察Delta复制策略所得到的复制误差具有一般性和实际意义。

Delta是衍生品领域最重要的希腊字母之一，它被定义为衍生品价格对标的资产价格变动的一阶敏感性，用数学公式表示可以写成

其中Δ为Delta，f表示衍生品价格。Delta复制策略的基本思想就是构造一个投资组合A，使其对衍生品标的资产价格在每时刻的一阶敏感性等于衍生品的Delta值，从而使得组合A的价值变动完全与衍生品的价值变动等价。从对冲风险的角度说，如果持有衍生品空头，同时持有组合A的多头，则每个时刻整个资产组合的价值变动就不再受标的资产价格变化的影响，从而实现了风险对冲；从复制的角度说，投资组合A就等于复制出了一个衍生品。由于Delta本质上是一阶导数，也就是价格曲线相应位置的切线斜率，衍生品的Delta值是时变的，因此Delta复制策略是一种时时调整的线性复制策略。

可以看出，Delta复制策略显然假设衍生品价格只依赖于标的资产价格，其复制成功与否、复制误差大小，对模型设定（例如是否为几何布朗运动）的准确性依赖度很高。模型风险的存在必然导致Delta复制误差。

在真实模型下，衍生品价格对标的资产价格的真实一阶敏感性可以表示为

其中表示衍生品的真实价格（TM表示true model）。但在近似模型M i下，衍生品价格对标的资产的敏感性却为

二者之差即为t时刻Delta复制策略因模型风险所产生的复制误差，误差值为

其中DE表示Delta error。在一段时间内，累积的Delta误差为[5](www.xing528.com)

很容易看出，在Delta复制策略中，只要存在Delta误差，即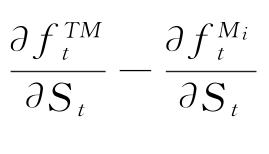不为零，Delta复制策略就无法完全对冲标的资产的风险。一旦标的资产的风险无法被完全对冲，对衍生品定价至关重要的风险中性假设就无法成立。然而在近似模型Mi下，仍会继续采用风险中性原理为衍生品定价，定价误差和模型风险相应产生。

为了进一步说明这一点，由于真实模型的复制成本等于初始定价，即

因此对式（3.1）做一些变换，可以得到

在BSM模型的框架下，式（3.2）中的近似等于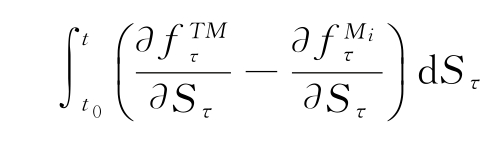，即累积的Delta误差。也就是说，复制误差，即交易员账户盈亏的一部分源自Delta复制误差，即模型设定偏误带来的误差。值得注意的是，由于这些复制误差完全由模型风险导致，因此无法通过改进复制策略本身[6]来避免。

那么，如何通过考察Delta误差来比较不同模型的模型风险呢？

从之前的分析可以看出，存在Delta误差时，风险中性假设不再成立，这样，标的资产价格在现实测度下的漂移率将对复制误差存在影响。换句话说，累积Delta复制误差会受到标的资产风险源的影响。因此，一方面，我们可以通过比较标的资产真实漂移率的变动对复制误差的影响来比较不同模型的模型风险，第4章就将通过数值模拟中对这个问题进行研究；另一方面，我们还可以通过考察标的资产真实漂移率的变动对Delta误差的影响，来研究现实中所使用的模型是否存在模型设定风险。第5章的实证中就将运用这个逻辑，将标的资产的收益率作为控制模型设定风险的变量。