衍生品定价中的风险与风险溢酬

由于在现实中，跳跃往往隐藏在股票价格中，因此，如何用市场上的股票价格的数据来区分股票价格中的连续扩散部分和非连续的跳跃部分一直是学者们探讨的热点之一。为了将股票市场上的跳跃鉴别出来，不少学者提出了各种方法来侦测跳跃。比如，Eraker Johannes and Polson（2003）[34]，Eraker（2004）[35]，Ait-Sahalia（2004）[36]，Barndorff-Nielsen and Shephard（2006）[37]，Jiang and Oomen（2008）[38]和Lee and Mykland （2008）[39]等。但其中不少学者的估计方法受到跳跃密度假设的影响，比如，Eraker Johannes and Polson（2003）[34]，Eraker（2004）[35]，Ait-Sahalia（2004）[36]。而Barndorff-Nielsen and Shephard（2006）[37]，Jiang and Oomen（2008）[38]和Lee and Mykland （2008）[39]的非参数方法不容易受到假设的影响。因此，这些非参数方法也成为近年来估计跳跃的主流方法，下文将对主要的非参数方法进行回顾。

2.3.2.1　BNS方法

Barndorff-Nielsen and Shephard（2004）[40]提出了双幂变差的指标，并通过这个指标构建统计量对标的资产的跳跃进行非参数估计。Barndorff-Nielsen and Shephard（2006）[37]将Barndorff-Nielsen and Shephard（2004）[40]的文章进行了扩展，提出了更多基于双幂变差的指标，用于对资产的跳跃进行估计。在Barndorff-Nielsen and Shephard（2006）[37]的文章中已实现的双幂变差（bipower variation，BPV）可以表示为

其中，y为瞬时收益率，而δ代表对于时间t的最小分割单位。Barndorff-Nielsen and Shephard（2006）[37]证明了，当δ→0时，双幂变差趋向于连续扩散部分的二次变差。而资产的已实现二次变差可以写成：

基于此，Barndorff-Nielsen and Shephard（2006）[37]构建了相应的统计指标，并给出了它们的渐进分布

其中

由于是一个不可观测的变量，因此，Barndorff-Nielsen and Shephard（2006）[37]建议用BPV作为它的估计值（用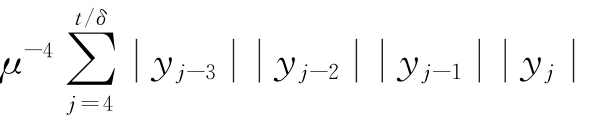作为代理变量）。代入式（2.24）和式（2.25）可以得到

根据这两个统计量，我们就可以判断在给定个股的收益率时，拒绝其是连续扩散过程的概率有多大。

然而，BNS方法也存在着一定的缺陷，比如，对于零收益数据极为敏感，当高频数据中出现零收益时，BNS方法中计算的RQV会被低估，这就对最后的统计结论有较大的影响。另外，BNS方法检验的是一段时间内是否发生跳跃，因此，它无法判断在某个点是否发生了跳跃，以及跳跃的具体大小、方向等。

2.3.2.2　JO方法

除了BNS之外，Jiang and Oomen（2008）[38]提出了用方差互换的方法来侦测跳跃。他们定义了方差互换等于

其中

S i/N为要侦测的资产的价格，由于已实现波动率可以表达成

再进一步，基于已实现波动率与互换方差的差异，Jiang and Oomen（2008）[38]提出了以下几个统计量

其中，V（0，1）代表[0，1]区间内的波动率(www.xing528.com)

通过式（2.28）和式（2.29）构造出来的统计变量的显著程度，我们同样可以判断出股票收益率序列是否发生了跳跃。

但JO的方法和BNS一样，在应用中也存在着一些不足。这两种方法的基本思路都是检验在一段时间内市场上的方差是否发生了异于以往的变化，因此，它们都只能描述一段时间内是否发生跳跃，而对某个时点是否发生跳跃或者在一段时间内的跳跃次数为多少都无法回答。所以，这两种方法都无法对跳跃的具体情况进行更深入的研究。

2.3.2.3　LM方法

Lee and Mykland（2008）[39]改善了BNS的方法，他们构造了在某一个时点能够侦测跳跃的指标

其中

此处，K是观测区间，在Lee and Mykland（2008）[39]的文中K＝16，并且，Lee and Mykland（2008）[39]推导出指标L（τ）经过变换后得到的指标ξ满足分布P（ξ≤x）＝exp（－e－x），而ξ可以通过以下式子得到

其中

其中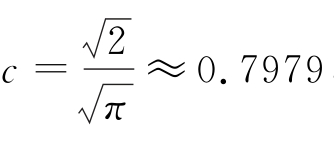，，n是每年的观测数。根据Lee and Mykland（2008）[40]，当ξ＞4.6001，即当指标ξ超过99％的临界值x∗＝－log（－log（0.99））＝4.6001时，我们认定证券价格发生了跳跃。

LM方法最大的优势就在于，其能够侦测到跳跃的具体时点，并且可以根据这个时点的跳跃进行进一步研究，比如分析跳跃的幅度、方向等信息。本书将在第5章使用LM方法检验股票市场上的跳跃。

2.3.2.4　跳跃风险的侦测在中国市场的应用

中国金融市场在短短20年的历史中，发生了多次剧烈的波动，尤其是近些年，如2007年5月30日、2008年1月22日与6月19日等，这些极端市场下跌有些是由于政策面的信息冲击，有些是由于外围经济环境的恶化，从而对中国金融市场造成的连带影响。这些跳跃风险给中国市场上的投资者带来了惨痛的教训，促使国内学者更加关注国内股票价格的跳跃行为。下文总结了国内学者对中国股市的跳跃行为所进行的相关研究[6]。

胡素华、张世英和张彤（2006）[41]以上证综指为样本用蒙特卡罗模拟——马尔科夫链（MCMC）的方法估计了的双指数跳跃扩散模型，他们认为双指数跳跃扩散模型可以很好地刻画国内市场尖峰肥尾的现象。汪先珍（2009）[42]运用Barndorff-Nielsen and Shephard（2004）[40]的方法估计了中国金融市场上股票资产存在的跳跃行为，并对跳跃的方差与市场总方差的关系进行了研究。陈浪南和孙坚强（2010）[43]用GARCH跳跃模型估计了国内外的一些重要指数，并对条件波动率与跳跃行为之间的关系进行了讨论。这些早期关于跳跃的研究仅对中国市场上的跳跃行为进行刻画，并没有涉及跳跃行为与收益率间的风险收益关系。

另外一部分学者已经开始关注国内金融市场上的跳跃风险会给收益率带来怎样的影响。左浩苗和刘振涛（2011）[44]对股票指数的跳跃方差与连续部分的方差进行分解，发现股指的跳跃成分以及跳跃波动率都会对未来的收益率起一定的预测作用。另外，Zhou and Zhu（2011）[45]运用LM方法和Fama-MacBeth全样本回归对分组后的组合收益率进行分析，发现在中国跳跃频率能够解释国内的横截面收益率，但他们没有检验跳跃频率是否是一个系统性风险，以及其有没有要求相应的风险溢酬。