衍生品定价中模型风险的相关研究

除了在不确定性框架下的研究外，不少学者也在风险的框架上对模型风险进行了具体的研究。他们的研究包括了模型设定误差带来的风险、参数估计错误带来的风险以及模型本身的差异对奇异期权的影响等。

Green and Figlewski（1999）[25]指出，在用BSM模型给期权定价时，波动率的变动反映了模型风险。他们研究了用历史波动率来预测BS的隐含波动率时，不同期限的历史波动率和不同的波动率模型的选择对各种金融衍生品定价带来的模型风险。Hull and Suo（2002）[26]指出为了描述市场上的模型风险，在对模型进行校准时就必须使用和交易员一样的连续校准（continual recalibration）的方式来对冲期权。他们检验了在股票的真实过程是随机波动率模型时，运用implied volatility function（简称IVF）模型（Dupire（1994）[4]）和运用BSM模型对奇异期权进行定价所产生的差别。他们发现在对复合期权和障碍期权的定价上，IVF模型都要优于BSM模型。但IVF模型在给障碍期权定价时，其误差较大，而在给复合期权定价时，其误差较小，这是由于尽管IVF模型能够在一个时点上较为精确的定价，但是却无法捕捉波动率的动态过程。Longstaff，Santa-Clara and Schwartz（2001）[27]认为如果用的模型是错误的，那么即使市场上交易员用的是每日校准模型的方法来设定模型的参数，模型设定的偏误同样会带来较大的定价误差。他们先将多因子的利率市场模型（LIBOR Market Model）作为基准，模拟市场数据，然后运用单因子模型通过每日校准来进行动态复制并对美式互换期权（American style swaption）进行定价。结果表明，单因子模型的每日校准无法弥补动态利率模型的设定偏误。以上学者的研究都证明了，模型的错误设定对定价的影响是不可忽略的，即使模型使用的参数随着信息量的增加而不断更新，错误模型的定价效果也无法很好地逼近真实模型。

Schoutens，Simons and Tistaert（2005）[28]比较了标的资产服从随机波动率模型、随机波动率跳跃模型、variance gamma（VG）、normal inverse gaussian（NIG）等几种过程时，收益与标的资产的k阶矩相关，即回报形式为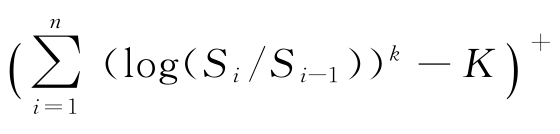[3]的衍生品定价。他们发现标的资产服从不同的过程，将导致收益为标的资产高阶矩的衍生品的不同定价差异。Schoutens，Simons and Tistaert（2005）[28]认为这揭示了为什么很多期权模型在刻画普通期权（vanilla option）的价格时都很相近，但是在为奇异期权定价的时候却产生了极大的差异。他的研究为不同模型之间的定价差异提供了最直接的证据，模型风险是和产品本身的属性有极大关系的，简单的产品使用不同的模型进行定价时，差异较小，而复杂的产品使用不同模型进行定价时，差异较大。产生这种现象的原因在于：

（1）在市场上，简单产品的流动性常常较大，因此可以作为校准的对象，而校准的目标函数本身就要求模型的定价误差较小。

（2）简单产品的回报常常仅与标的资产到期时刻的分布相关。这意味着即使一个模型无法很好地刻画标的资产在不同时点边缘分布之间的相关关系或者标的资产高阶矩的特点，只要它能够近似描述出到期时点的标的资产价格的分布，就能够较为准确地定价。但这样的模型显然无法精确地给某些复杂衍生品定价，如路径依赖或高阶矩衍生品。(www.xing528.com)

（3）复杂的产品的价格对未来信息的冲击更加敏感，这意味着模型的参数变化可能会过于频繁，模型风险对复杂产品的影响要比对简单产品的影响更大。

Frey（2000）[29]认为在对衍生品进行复制的时候，流动性导致的复制偏差是导致模型风险的一个重要原因。因此Frey在假设了对冲行为会对标的价格产生影响后，在BSM模型的基础上发展出了考虑流动性因素的期权定价模型。在考虑了流动性的影响后，期权的价格满足一个非线性偏微分方程。Frey的研究表明，真实市场和理想市场的差异将导致模型的差异。同样，市场上不可忽略的交易费用（Leland（1985）[30]）、无法实现的时间无限可分以及交易带来的时滞等都有可能导致理想市场中的理论模型在真实市场中不适用，从而带来模型风险。

Detlefsen and Härdle（2007）[31]通过比较最小化期权校准函数，发现不同校准函数会对定价产生较大的影响。最小化相对隐含波动率误差而言，其所得到的价格在其他的指标下（最小化绝对价格误差、最小化相对价格误差、最小化绝对隐含波动率误差）表现相对良好并且比较稳定，因此他们认为最小化具有较小的校准风险（calibration risk）。但是，最小化将导致不同模型间的定价差别加大，具有较大的模型风险。而最小化绝对价格误差具有最小的模型风险，但是有最大的校准风险。因此市场上的交易员在选择校准函数时，必须在模型风险和校准风险之间进行权衡。Detlefsen and Härdle（2007）[31]的研究表明，在面对同样的市场数据时，不同的优化目标函数和误差函数的权重等都可能会导致同样的模型在实际复制时出现较大差异。

可以看到，在风险框架下进行的这些研究大多都从某个细节入手，间接地证明了与模型风险以及复制误差相关的要素有哪些。