对储备币种的相关研究的另一个重要分支就是均值—方差分析法。马柯维茨(1952)[149]资产组合模型利用均值—方差模型分析得出通过投资组合可以有效降低风险的结论。MV模型研究对象是具体的国别,而不是世界总体和区域的总量情况。
马柯维茨的资产组合理论的核心是:金融财富的持有者将根据各资产的收益和风险将其财富分布在各资产上。MV模型假设证券市场有效、投资者具有风险厌恶特征、投资者会选择无差异曲线(代表自身的风险偏好)与有效边界(在收益率的期望值一定的条件下风险最小的资产组合构成)的切点作为最有风险资产组合。资产组合理论的运用的基本分析法是均值—方差分析。
(一)资产组合的预期收益
在均值—方差分析中,资产组合的预期收益等于每一种资产的预期收益的加权平均,表示为:
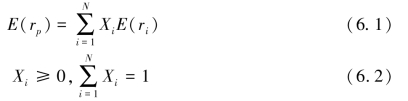
式中,rp表示包含在资产组合中的各种资产的预期收益的加权平均数;
E(rp)表示资产组合的预期收益;
Xi资产组合中资产i所占的权数;
E(ri)资产组合中资产i的预期收益;
N为资产种类。
(二)资产组合的预期风险
1.方差。资产组合的风险不仅与每种资产的风险有关,而且也受资产之间相互关系的影响。风险是指资产收益的不确定性,即遭受损失的可能性,因此风险的大小可以用预期收益率的方差来表示。标准差是各种可能的收益率偏离期望收益的综合差异,是用来衡量资产收益风险程度的重要指标,方差越大,风险越大。
方差:
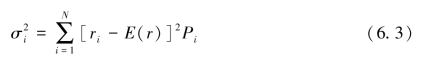
标准差:
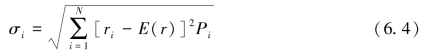
式中,ri为N个观测到的收益值的一个;
Pi为各个收益率ri出现的概率;
E(r)为收益率的期望值。
2.协方差。资产组合的风险不同于单个资产的风险,除与方差有关外,还与协方差和相关系数有关。协方差是衡量两个随机变量如资产i的收益率和资产j的收益率的互动性的统计量,协方差标准化的结果就为相关系数。两种资产之间的协方差是描述两种资产相关性的指标。如果协方差为正,表示两种资产的收益率倾向于同一个方向变动,即一种资产的实际收益率高于期望收益率可能伴随另一种资产的实际收益率高于期望收益率。反之,表示两种资产之间存在一种反向变动的关系,一种资产收益率的上升可能伴随着另一种资产收益率的下降。一对相对较小或者为零的协方差表示两种资产的收益率之间只存在很小的互动关系或者没有互动关系。资产之间的协方差越大,它们组成的资产组合的风险越大。
协方差:
![]()
式中,COV(ri,rj)表示资产i和j收益率之间的协方差,ρij表示i和j收益率之间的相关系数。
3.相关系数。两种资产收益率之间的相互关系还可以用另一种统计量来表示,那就是相关系数。假定σ(ri)、σ(rj)分别为资产i和资产j的收益标准差,COV(ri,rj)是两种资产之间的协方差。
![]()
当ρij=0时,表示两种资产之间的收益不存在线性相关关系,但是不排除存在其他非线性的相依关系。当ρij=1时,表示两种投资资产之间存在完全的线性关系。一般来讲,如果ρij<0,可能降低组合后的风险,反之,则会加大组合后的投资风险。
由于外汇储备的币种管理问题就是资产的组合问题,因此可以利用MV法的资产组合技术分析央行的币种选择问题。将央行视为投资者,货币当局持有的国际储备资产视为资产组合。在一定的约束条件下,寻求央行管理的目标最大化的最优货币组合。理性政府的政策目标有以下两种情况:收益既定下风险最小化;风险既定下收益最大化。MV分析方法主要考虑风险和收益两种因素,认为资产组合理论的有效运用,取决于构成该资产组合的金融资产按某种比例组成一篮子商品的预期价值及价值的波动性。由于风险的存在,理性的货币当局不会把所有储备资产放在某种收益率最高的币种上。从投资的角度来说,收益率越高的商品,往往风险也越大。因此需要分散风险,以实现政策目标的最大化。
(三)资产投资的有效组合
当投资者面对众多可以选择的组合方式时,如何进行组合,通过改变不同资产的权重,实现既定收益下风险最小或者既定风险下收益最大呢?马柯维茨利用期望收益率方差资产组合模型来解决资产的选择和配置问题。
1.无差异曲线。投资者在进行资产投资和配置之前,都会考虑自己的风险偏好程度。一条无差异曲线在相同效用的情况下,不同的风险和收益组合,在一条无差异曲线上,相对于投资者来效用是相等的。
无差异曲线有以下特点(见图6.1):第一,对于每个投资者来说,都有无数条无差异曲线表示其对风险和收益的偏好,位于上方的无差异曲线的效用要高于下方的无差异曲线效用;第二,每条无差异曲线都是上升的,因为投资都是风险厌恶的,让他承受更高的风险,必须支付更高的收益;第三,对于投资者来讲,无差异曲线上升的速度是递增的。这就是说随着风险的递增,投资者的风险厌恶程度是上升的,需要支付更高的收益。
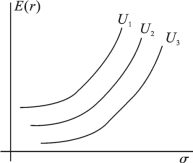
图6.1 无差异曲线
此外,从无差异曲线还可以看出投资者的风险厌恶程度,高度风险厌恶者的无差异曲线往往比较陡峭,轻微风险厌恶者无差异曲线要平缓一些。这是因为高度风险厌恶者承担更多一单位的风险,它要求的收益要大于轻微风险厌恶者的要求。
2.有效市场边界。有效市场边界是投资者评价的客体,有效边界就是资产的有效组合。图6.2中的阴影部分就是所有可能的资产组合,就是可行集。但是并不是所有的组合都要考虑,投资者只需考虑可行集中的一个子集。投资者选择的最优资产组合要从下列组合中选取:(1)对每一水平的预期收益,该组合能提供最小的风险;(2)对每一水平的风险,该组合能提供最大的预期收益。满足这两个条件的组合就是有效集,称为有效市场边界。图中A点具有最小标准差,即A点的风险在可行集中最小,B点的预期收益率最高,夹在A和B两点之间的边界部分就是有效市场边界。投资者考虑有效市场组合时,只考虑有效市场边界这个子集就可以了,因为只有在有效市场边界上才能满足以上两个条件。

图6.2 可行集
3.最优投资组合的选择。通过以上分析可以看出,投资者要在有效市场边界上选择最优投资组合。至于选择哪一个点进行投资,是由投资者对风险和收益的偏好所决定的。投资者可以借助有效市场边界和无差异曲线来进行最优投资组合的选择(如图6.3),无差异曲线和有效市场边界的切点就是最优资产组合。
 (https://www.xing528.com)
(https://www.xing528.com)
图6.3 最优资产组合
根据无差异曲线和有效市场边界的切点P,找到最优资产组合,P点构成了最佳投资组合。我们知道无差异曲线是下凸的,有效市场边界是下凹的,这样保证了切点的唯一性。
(四)均值—方差模型的数学求解
1.马柯维茨模型的数学表述。根据马柯维茨模型的思想,投资者需要找到一个最佳的投资组合,满足投资者在收益和风险下的平衡。于是,马柯维茨提出了均值—方差模型。
假设某个投资组合有N种不同的风险资产,第i种资产的预期收益为E(i),方差为σ2i,i=1,2,…,N,它在资产组合中的权重为xi,且

则投资组合的期望收益和方差为:
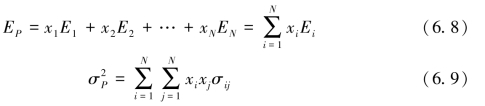
式中,当i≠j时,σij表示协方差,当i=j时,σij=σ2。把(6.9)式转换为:
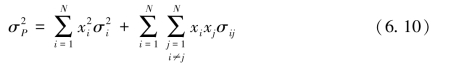
马柯维茨根据经济人是理性人的假设,认为投资者在资产投资过程中,力求做到在收益既定的条件下风险最小,或者在风险既定的条件下收益最大。
(Ⅰ)既定组合收益下,风险最小化。
给定既定收益EP=E0,得到:
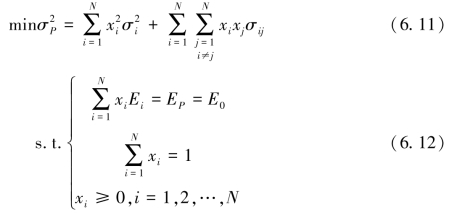
(Ⅱ)风险既定下,收益最大化。
给定组合风险σ2P=σ20,得到:
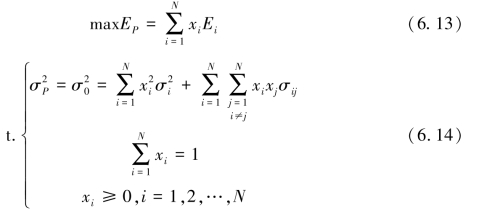
2.用拉格朗日方程求解马柯维茨模型。
对模型(Ⅰ)和模型(Ⅱ)求解时,可利用拉格朗日函数进行求解。
(1)模型(Ⅰ)的求解。
为解模型(Ⅰ),引入拉格朗日算子λ1和λ2,建立拉格朗日函数,如下:
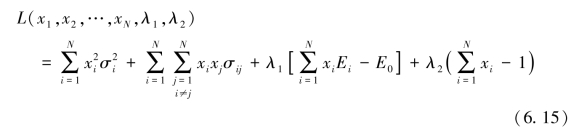
对拉格朗日函数分别对x1,x2,…,xN,λ1,λ2求偏导,其令其等于0,得:
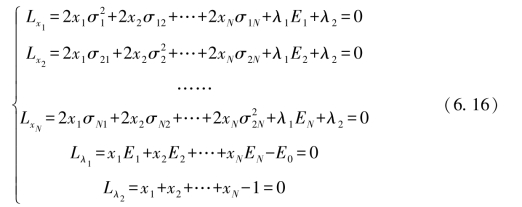
上述方程共有N+2个未知数x1,x2,…,xN,λ1,λ2和N+2个方程,由此可解出,x1,x2,…,xN的解,用通式表示为:
![]()
可见在给定的收益率水平下,计算出不同资产的权重,从而得到风险最小的组合。给定不同的收益率,就会得到不同的资产组合形式。根据不同的E0确定的资产组合形式组成的子集就是有效市场边界。
将上述方程组写为矩阵形式为:

(2)对模型(Ⅱ)的求解。
由于不同投资的风险偏好不同,引入风险偏好系数μ,当μ=0时,表示投资者为风险喜好型。当μ趋向于无穷大时,表示投资者为风险厌恶型。引入拉格朗日算子λ,写出拉格朗日函数:
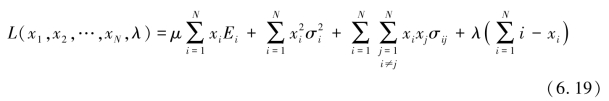
对拉格朗日函数分别对(xi,x2,…xN,λ)求偏导数,并令其等于零,可得到在既定风险水平下,收益最大的资产组合形式。
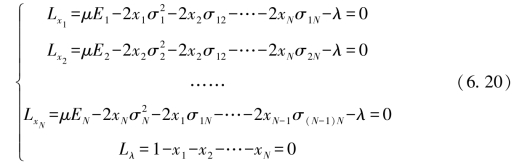
上述方程有N+1个未知数和N+1个方程,能够得到方程解,通式为:
![]()
把不同的风险规避系数代入就可到每种资产权重的具体解。将上述方程写为矩阵形式:
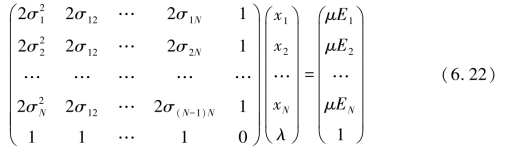
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




