金融资产利率风险衡量方法及注意事项

目前主要采用的金融资产利率风险衡量方法有缺口分析法、持续期、凸度。

（一）缺口分析法

缺口是用货币表示的利率敏感性资产（RSA）和利率敏感性负债（RSL）的差额，用公式写为：

缺口分析法经常被用于对资产和负债对利率的敏感性进行测量，当利率敏感性资产大于利率敏感性负债时，金融机构处于正缺口；反之，如果利率敏感性资产效益小于利率敏感性负债时，金融机构处于负缺口。对于一个投资主体来说，只要存在缺口，不论是负缺口还是正缺口，都表明利率敏感性负债和利率敏感性资产不平衡。短期利率的波动对资产价值和收益都会产生影响，且对资产价值和收益的影响与对负债价值和成本的影响不能互相抵消，因而该投资主体的经济利益就会受到利率不确定性的影响，从而面临利率风险的威胁。我国外汇储备资产作为一种金融资产，也会受到利率风险的威胁。

用缺口的绝对值乘以利率的变动量可以得到净利息收入的变动量，也就得到利率对投资损益的影响大小。其计算可以表示为：ΔNI=|GAP|×Δr。

（二）持续期

上述缺口分析法并没用考虑到利率的敏感性以及资产组合证券有效期限不同对利率敏感性的差异。因为期限越长的债券的价格和回报率波动受利率影响要远远大于短期债券，因而传统的缺口分析法并不能准确衡量利率的不确定性对资产和负债可能产生的影响。相对于传统的利率风险衡量方法，持续期能更加有效地衡量利率水平波动对债券和资产负债的影响，因而它相对于缺口分析法是一种更为有效的测量利率风险的工具。

1.麦考利久期。期限越长的债权，其价格受利率波动的影响越大，因此债券的期限结构可被视为衡量利率风险的合理尺度。由于有些债券并不是在某个确定的到期日偿还，而是分批偿还本息，所以不能简单地用距离到期日的时间长短来衡量利率风险大小，因此引入久期的概念。需要注意的是，对于到期日与持有期一致的短期债券不存在利率风险。

久期分析的基础是麦考利（1938）提出的久期概念，它能够衡量证券支付流动的平均寿命，且能近似估计证券市值对利率变动的敏感性。计算公式为：

式中，t为收到现金流的时间，i为到期收益率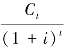，为证券到期收益率的贴现值，T为距离到期日的时间，C为在时间点t的现金流（包括利息与本金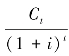），为证券现金流的总现值。

由（4.29）（4.30）可知，麦考利久期分析实际上是以未来一系列现金流的现值占现金流的总现值的比率作为加权数计算的平均持续期，来考查利率变动对资产净值的影响。麦考利久期具有以下特点：

（1）除了零息债券的持有期与到期日相同外，其他债权的持有期都比到期时间短。

（2）当利率不变时，债券持续期会随着到期期限的增长而增长。到期日短的债券持续期短；反之，持续期长。

（3）对于到期日相同的债券，持有期与利率反向变动，利率下降持有期延长。息票利息率高的债券期短，反之，持续期长。

（4）在其他因素不变的情况下，持续期与收益率成反向变动，收益率高持续期短。(www.xing528.com)

2.债券价格与持续期。麦考利久期公式虽然可以通过久期度量证券的相对利率风险，但是却无法直接表达利率发生变动时，证券价格将发生多大的变动。运用现值和久期计算公式可以得出证券市值与持续期的直接关系。

我们对（4.31）式i求导：

根据久期的计算公式，得：

根据（4.32）式说明，证券市值变动的百分率与久期之间的数量关系。证券的持续期决定证券市值相对于收益率变化的敏感性。持续期越长，证券市值的利率敏感性越大，持续期成为利率风险暴露的测度方法。

如果在（4.32）式中加入修正的久期概念，把修正的久期D∗定义为：

（4.30）式变为：

（4.35）式说明，证券市值变化的百分率等于修正的久期与证券到期收益率变化的乘积。

3.证券组合的久期。对于多种资产和负债组成的资产组合，用久期来度量利率风险将变得稍微复杂一些。可以通过两种办法：一是首先计算证券组合中每一种证券的久期，然后以组合中每种证券的市值为权数计算这些证券久期的加权平均数的证券组合的久期；另一种方法是将证券组合作为一种证券，将证券组合的现金流视为证券的现金流，根据设想的这一种证券的现金流计算得到的久期就是证券组合的久期。但是，这两种计算证券组合久期的方法和结果并不同，当有上升的收益率曲线时，第二种算法较准确；当市场利率下降时，第一种算法较准确。因此在估算证券组合的利率风险时，必须根据实际情况选择合适的计算方法，否则，将会产生不准确的计算结果。

（三）凸性

久期反映了利率与证券价格之间的近似线性关系，主要度量证券市值—收益率曲线斜率，凸度通过对该曲线的弯曲程度进行测量，可以度量出近似线性所产生的误差，从而比久期分析法能更加准确地反映出利率与证券市值的变化关系。

债券的凸性是衡量久期怎样随收益率变化的二阶结果。从数学上来讲，凸度是债券价格方程对收益率的二阶导数再除以价格得到：

然后我们把债券回报率与债券价格变化率用泰勒级数亮相扩展式展开：

因为无期权债券的凸度是正数，所以当利率下跌时，凸度使久期变长，债券价格加速上升；相反，当利率上升时，凸度使久期变短，债券价格以减速度下降。