【摘要】:为了直观地理解风险损失之间的相关性,在图5-2中给出了不同相关结构下的风险损失率三维散点图。根据总的风险损失率zi=i和1000次蒙特卡洛模拟的结果,我们可以得到总风险损失率序列。风险集成是为了说明金融机构在风险相关下总风险损失率,总损失率是在考虑了相关性以后各种风险损失率的总和。表5-4不同相关结构下模拟总风险损失率的统计特征
由于本文关注的是在相关结构下风险的损失,所以每一种风险损失不是单独的对总的风险损失起作用,而是通过相关关系来实现单一风险损失对总损失的影响。为了直观地理解风险损失之间的相关性,在图5-2中给出了不同相关结构下的风险损失率三维散点图(100000个模拟值)。本文使用不同的Copula函数每次产生100000个随机样本,得到需要的分位数,然后模拟1000次,并计算1000个分位数的平均值,得到相对稳定的值和分位数。根据总的风险损失率zi=(w1y1+w2y2+w3y3)i和1000次蒙特卡洛模拟的结果,我们可以得到总风险损失率序列。风险集成是为了说明金融机构在风险相关下总风险损失率,总损失率是在考虑了相关性以后各种风险损失率的总和。
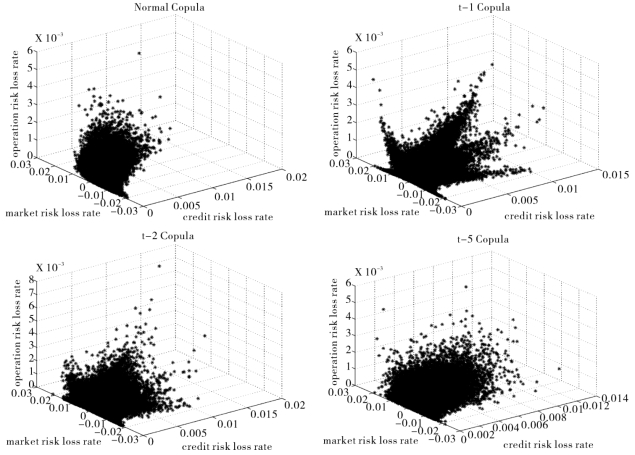
图5-2 不同相关结构下风险损失率的三维散点图(https://www.xing528.com)
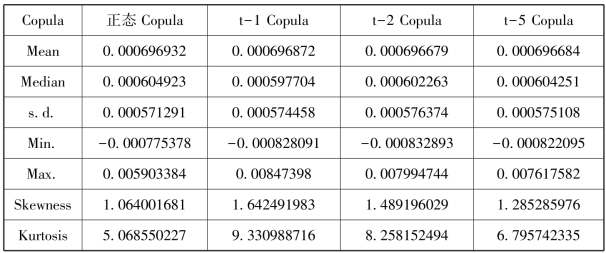
从表5-4我们看到,在不同的Copula关系结构下,均值比较相近;标准差存在一定的差异;由于经验分布都有偏,偏度都大于0,均是左偏;总损失率分布都存在厚尾的现象,因此所有的峰度都大于3。总损失率的均值趋于一致,而不同相关结构类型下具有不同的总损失率分布,偏度和尖峰厚尾的特征值存在很大的差异,由此我们估计总风险对相关结构是敏感的。
表5-4 不同相关结构下模拟总风险损失率的统计特征
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




