中国金融稳定性研究：数据来源及相关参数

由于我国缺乏完整的金融企业的市场风险、信用风险、操作风险的公开数据源，本文拟直接运用和采纳已有的研究成果给出的风险分布的参数数据。

1.三种风险的损失率分布和各自的分布参数

我们采用Elsinger和lehar（2006）得出的奥地利银行业的风险分布结论来研究风险集成问题。本文所用数据包括：市场风险、信用风险的均值与方差和操作风险分位点，具体见表5-1。

表5-1　不同风险损失率分布参数的估计结果

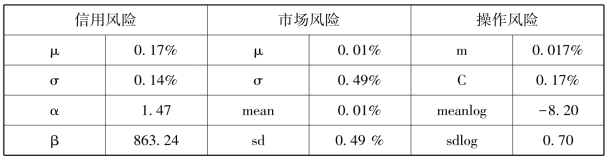
数据来源：Elsinger和lehar（2006）和李建平、丰吉闯、宋浩和蔡晨（2010）。

根据各个风险损失率分布和相应的参数，使用Matlab7.8可以做出模拟损失分布密度图，见图5-1。

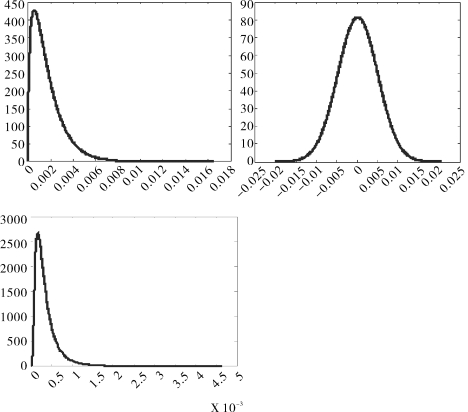
图5-1　信用风险、市场风险和操作风险损失率边际分布图(www.xing528.com)

从图上我们可以看到各不相同的风险损失分布，市场风险呈现出对称性，而信用风险和操作风险是有偏的分布，呈现出尖峰厚尾的特点。

2.相关系数和业务权重数据

信用、市场和操作风险之间的相关系数是运用Copula进行风险损失模拟的前提条件，本文采用Rosenberg和Schuermann（2006）统计的银行业信用风险、市场风险和操作风险之间的相关性系数的均值和业务权重，具体见表5-2、表5-3。

表5-2　信用、市场和操作风险之间的相关系数

数据来源：Rosenberg和Schuermann（2006）。

表5-3　信用、市场和操作风险业务权重

资料来源：Rosenberg和Schuermann（2006）。