后金融危机时期的中国金融稳定性研究及其思考

1.信用风险在银行部门间转移

在前面的部分，我们假设风险转移到不具有脆弱性的部门。从稳定的角度来看，风险仅仅是消失。然而，实际上，稳定性几乎会因风险购买者承担风险增加而受到影响。我们在后文将会对此进行分析。首先研究信用风险在银行部门内部转移，然后研究信用风险跨部门转移。缺乏信用风险转移的证据说明各种形式的信用风险转移是相关的。例如，Fitch Ratings（2003）在报告中指出，一个显著的净资产风险转移来自银行部门信贷风险，绝大部分转移到保险部门。然而，他也指出有大概90%的信用衍生工具欠款由银行持有。由于银行在事前分析是一致的，对于信用风险转移的激励仅仅来自于分散公司特质风险。因此，我们直接考虑那些允许银行对他们所在区域要求权与公司总风险进行互换的信用风险转移。这种互换由中介机构提供，他们从银行购买该地区的要求权，然后通过向银行购买风险保护来对冲总风险。由于中介机构通过大数法则持有银行创造的资产的总风险暴露，他可以通过这种方式创造一个无风险头寸。中介机构在这一互换中的预期收益是

中介机构的竞争力表明互换的价格是p＝wB

用q（0≤q≤1）代表银行通过互换分散的区域特质风险所占比例，银行的资产组合在t＝1时候是：

因此企业产出的银行价值是：

与前文类似，有最优的q可以表达为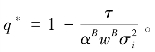与前文中信用风险转移表达式比较我们可以发现当时，对于给定的τ，信用风险转移的程度会降低。这是因为在银行内部的信用风险转移不能使银行分散总风险，所以增加转移一单位的信用风险转移获得的收益将降低。如果两种方式的信用风险转移成本均相同，这是因为信用风险转移减少。信用风险转移后的资产组合方差(σB)2是：

信用风险因此比前文计算的更高。这是两个原因造成的：第一，总风险不能在银行内部分散，这是为什么银行风险有额外的部分；第二，正如前文所讨论的，因为从信用风险转移获得的利益降低，信用风险转移将会减少。因此由于我们得出引理4和论点1。

引理4　wB′(τ)／wB＜－1

论点1　银行内部信用风险转移成本的降低将会带来效率的增加但最终会减少稳定性。

证明：有效性：类似于评述1的证明。稳定性：(σB)2对τ求导，可得到：

这里用引理4代替wB′(τ)。如果τ足够小，方程（2-27）将不成立。

效率的结论是对评述1进行讨论的结果：τ的减少将会减少信用风险转移，因此会减少银行要求的风险溢价。对稳定性的影响是较复杂的也是模糊不清的。正如显示的那样，银行风险将不仅仅是初始资产组合的地区特质风险（与前文原因相同），但是仍然完全包含初始的系统风险后者明显是因为系统风险不能在银行内部分散。如果银行额外承担的风险足够大，那么增加的系统风险可能增加了地区特质风险分散对稳定性的影响，使得信用风险转移不再稳定。论点1也指出如果τ持续降低，那么最终稳定性也会降低。直观的，这是因为当τ降低分散对于稳定性的影响将会变小（并且最终变为0），尽管增加的承担风险并不会降低到一个特定的（积极）水平（如引理4展示的）。

2.跨部门信用风险转移

我们考虑信用风险在银行和非银行金融部门间转移（与第三部分相比），并且考虑非银行金融部门的稳定性：αN≥0，βN≥0。我们的信用风险转移市场模型如下：银行出售它们的地区要求权给中介，然后将仅仅持有的系统风险转而出售给非银行金融机构。用qB代表银行出售的资产部分，我们在t＝1时持有的银行资产组合类似于基点：

非银行金融机构的资产组合由它们初始持有的公司股权（只有系统风险，而非系统风险被分散掉了）加上信用风险转移时购买的公司要求权减去价格(www.xing528.com)

这里qN表示购买的公司系统风险的数量（用银行资产组合的比例来表示）。

引理5　信用风险转移的均衡由下式决定：

银行和非银行金融机构的风险是：

对于银行内部信用风险转移，信用风险转移成本的下降会导致信用风险转移的增加和银行风险的降低，然而，现在会带来非银行金融机构风险增加的成本。相比于银行内部风险转移，跨部门风险转移的程度是多少？假设没有系统风险，代入（2-30）有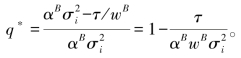因此，信用风险转移决定于两个部分。第一部分决定于αBb－αN (1－b)，即不同金融部门的公司风险的加权差。如果这个差值为正，那么就存在着将风险向非银行金融机构转移的激励。然而，这并不意味着存在着信用风险转移的成本时，信用风险转移也会增加。与前文类似。第二部分表明当信用风险转移成本增加时信用风险转移降低。信用风险转移将会增加（因此比在银行内部信用风险转移多），如果加权风险差比信用风险转移成本大得多。

相较于在银行内部进行信用风险转移，跨部门信用风险转移的优点是什么？我们分析证明跨部门信用风险转移更加好。首先，它允许风险向风险较小的非银行金融机构转移。其次，相较于在银行内部进行信用风险转移，它使得银行承担的额外风险被完全分散。

我们现在简化分析，假设k和e（即f）是不变的常量。

论点2　对于固定产出f，跨部门信用风险转移成本的降低将会导致对于所有的τ有稳定性的增加，当且仅当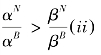，总会有效率的提升。

论点2说明，为了进行信用风险转移需要提高稳定性，风险从系统风险较高的部门转移到较低的部门是不够的（我们分别用α和β来指代特质风险和系统风险）。为了证明这一点，我们假设βB＞βN，αB＞αN并且b＝1－b＝1／2，即银行部门的系统风险和特质风险都高于非银行金融部门，而且这两个部门的规模是相同的。既然αB＞αN，由于非银行金融机构加权风险高于银行部门，那么就存在着一个风险流向非银行金融机构的趋势。金融系统的不稳定性将带来各个部门的风险增加［方程（2-16）］，不稳定最小化类似于两个不相关的资产组成的资产组合最优化：进行投资的两个资产的组合方差最小化（虽然风险比较低的资产投资较多）。风险流向非银行金融机构可能因此带来银行承担的风险“更小”。

前面的讨论证明信用风险转移只与稳定性提高有关，因为相关的特质风险并不会带来社会效率的显著提高。因此，存在一个监管的范围。监管可以以资本要求的形式纳入我们的框架中：资本要求是银行被要求在危险增加时必须持有的资本的增加，如同破产成本，把银行风险成本化并因此影响银行的积极性。我们可以将αB和αN解释为受两个因素影响：破产成本和资本要求带来的成本。由于破产成本独立于资本要求，因此监管可以通过资本要求设置为水平α（较大的α代表严格的资本要求）。

论点3证明了监管者如何设置跨部门的α比例r，如果他们想要稳定性最大化，

论点3　对于固定产出f，最优监管比例r（稳定最大化）是：

因此，如果βN＜βB，监管最优化带来监管套利（αN／αB＜1）。进一步的，最优监管套利超过了相对外部性（αB／αN＞βB／βN）。

因此，正如前文所讨论的，没有信用风险转移成本（τ＝0）时，我们有r∗＝βN／βB，即最优监管比例保证特质风险成本与系统风险成本相等。然而，如果信用风险转移有成本，从社会视角来看，监管将导致信用风险转移不足，即银行承担信用风险转移成本因而减少转移。为使稳定性最大化，最优监管比例应为超过跨部门系统风险的比例，以弥补存在信用风险转移时，银行因激励不足而减少的信用风险转移。

为了得到这些结果，我们假设k和e（即f）是外生变量；因此金融系统的总融资额是已知的。如果f可以调整，那么信用风险转移的成本降低将会带来总融资额的增加，这是因为在金融部门中风险可以更好地分散而带来风险溢价的降低（正如前文所讨论的）。这将因此带来效率的提高和金融系统增加的风险的成本。从原理上来说，监管将因此提高各部门的资本要求（尽管由论点3可知保留监管套利来保证跨部门风险最优分配）来减少承担额外的风险。然而，从福利学角度来看，这种监管并没有明确的保证，因为信用风险转移的增加将会限制效率。