图书馆职业能力研究：基于因子分析的调查结果

在对高校图书馆学科服务能力要素调查问卷进行因子分析时，要求变量间应具有较强的相关性。在对调查问卷进行KMO和Bartlett检验后发现，KMO数值为0.894(见表5-1)，大于0.8的要求，显著性水平为0.000＜0.05，表明变量间有共同因子的存在，适合进行因子分析。

表5-1　KMO和Bartlett的检验

利用主成分分析法来萃取因子。在不限定萃取因子的个数时，可以得到10个共同因子。但在这10个共同因子中，一些因子包含的成分(即题项)较少，还有一些因子包含的成分比较杂乱，无法从中找到共同特征并进行命名。因此，在后续的因子分析中，依次限定共同因子的个数为9、8、7、6、5、4个。当限定萃取因子的个数为4个时，因子分析的结果较为理想，此时解释的总方差为55.859%(见表5-2)，高于50.000%，符合要求。

表5-2　因子解释的总方差

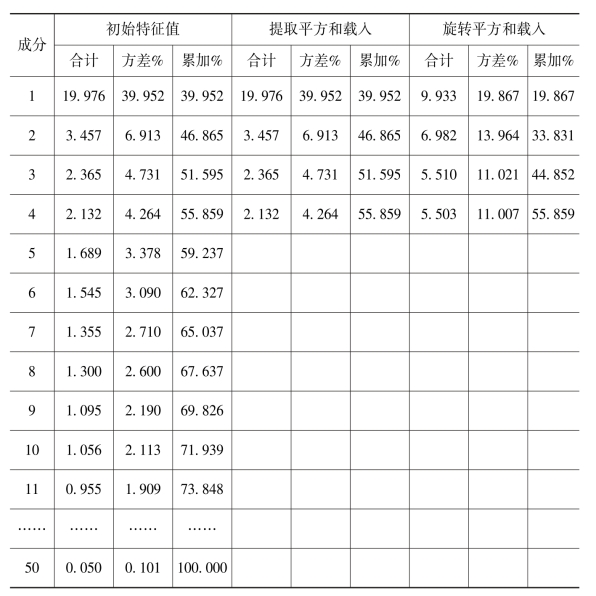
注:提取方法为主成分分析法。

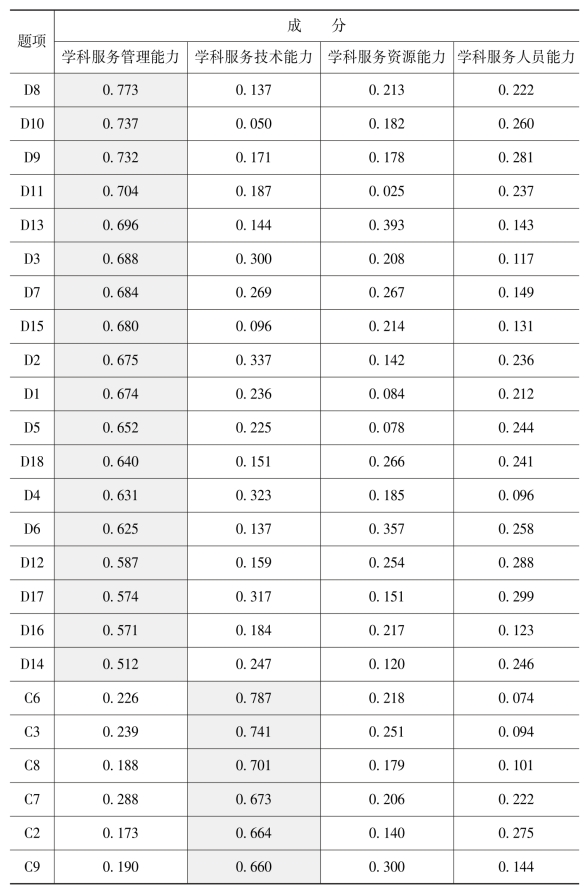
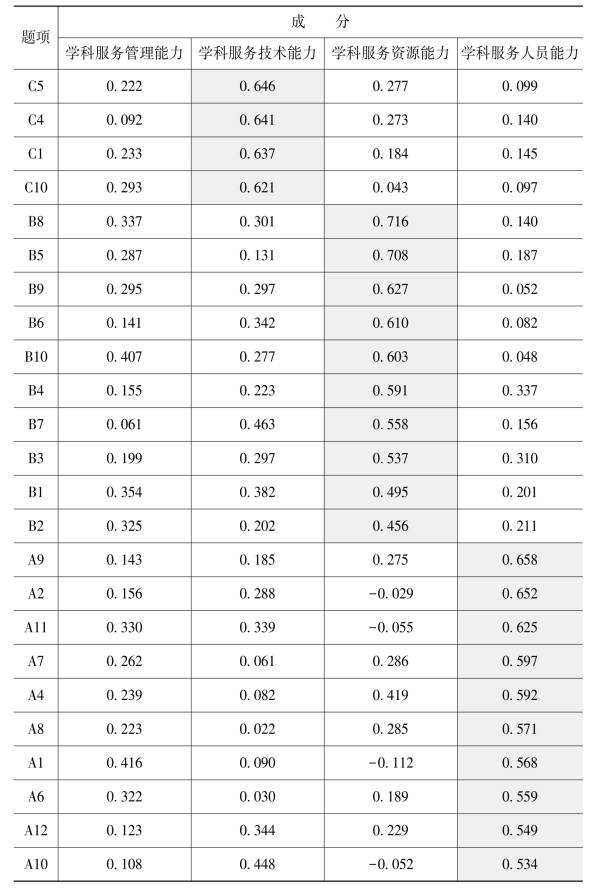
利用主成分分析法和Kaiser标准化正交旋转法，可以得到这4个共同因子的旋转成分矩阵(见表5-3)。其中，因子1包含18个题项，即D1-D18，可命名为“学科服务管理能力”；因子2包含10个题项，即C1-C10，可命名为“学科服务技术能力”；因子3包含10个题项，即B1-B10，可命名为“学科服务资源能力”；因子4包含12个题项，即A1-A12，可命名为“学科服务人员能力”。(www.xing528.com)

表5-3　旋转成分矩阵

续表

续表

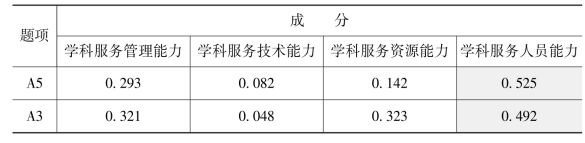
注:提取方法为主成分分析法，旋转方法为Kaiser标准化正交旋转法，旋转在7次迭代后收敛。