高考导航
1.不等式选讲内容,在高考题中以选做的形式出现,难度一般不大,比较近三年的高考题,出现频率较高的有:解绝对值不等式,作含绝对值的函数图像,含参的绝对值恒成立有解问题,不等式证明等,方法多样,注重对学生数学核心素养的培养.
2.不等式选讲是新课标的新增内容,也是其选考内容.从能力要求上看,这部分主要考查学生了解不等式、应用不等式的能力,以及分析问题和解决问题的能力.
(1)考查含绝对值不等式的解法与含绝对值符号的函数的最值、恒成立问题.
(2)考查不等式的证明,会用综合法、分析法等证明不等式,往往难度不大,加以适当的训练是完全可以掌握的.
例题精析
【例1】(2017年全国Ⅲ卷理数)已知函数f(x)=|x+1|-|x-2|.
(1)求不等式f(x)≥1的解集.
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.
▶ 解题指南
(1)对x的取值范围分段讨论得到x在不同区间上的函数表达式,每段分别求解不等式后对各段解集取并集,从而可得到原不等式的解集.
(2)依题设可将问题转化为求函数的x最大值,则只要m小于等于函数的最大值即可.结合(1)可得到函数g(x)的分段表达式,在每段上分别求函数的最大值,最后得到函数g(x)在整个实数集上的最大值,即可求得m的取值范围.
▶ 解析
(1)方法一(分类讨论法):

当x<-1时,f(x)≥1无解;
当-1≤x≤2时,由f(x)≥1,得2x-1≥1,解得1≤x≤2;
当x>2时,由f(x)≥1,解得x>2,所以f(x)≥1的解集为{x|x≥1}.
方法二(数形结合法):

因为f(x)=|x-1|-|-x-2|≥1,画出函数f(x)的图像(见图9.1).
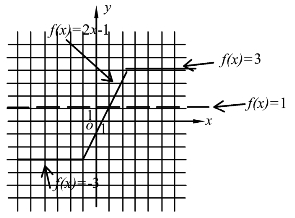
图9.1
f(x)≥1的解集为{x|x≥1}.
(2)由由f(x)≥x2-x+m,得m≤|x+1|-|x-2|-x2+x,而



规范解答



巩固提高
1.设函数f(x)=|2x+1|+|x-1|.
(1)画出y=f(x)的图像;(https://www.xing528.com)
(2)当x∈[0,+∞),f(x)≤ax+b,求a+b的最小值.

▶ 解题指南
(1)根据x的取值范围,去掉绝对值符号,即可得到f(x)的解析式,再根据解析式,即可画出f(x)的图像;
(2)根据题意y=ax+b的图像在f(x)图像上方,所以b≥2,a≥3,当a,b同时取最小值时,a+b最小.
2.设函数f(x)=5-|x+a|-|x-2|.
(1)当a=1时,求不等式f(x)≥0的解集;
(2)若f(x)≤1,求a的取值范围.
▶ 解题指南
(1)先根据绝对值几何意义将不等式化为三个不等式组,分别求解,最后求并集.
(2)先化简不等式|x+a|+|x-2|≥4,再根据绝对值三角不等式得到|x+a|+|x-2|的最小值,最后解不等式|a+2|≥4得a的取值范围.
3.已知函数f(x)=|x-a|+|x+1|.
(1)若a=2,求不等式f(x)>x+2的解集;
(2)若关于x的不等式f(x)<2的解集不是空集,求实数a的取值范围.
▶ 解题指南
(1)若a=2,由绝对值不等式分数讨论得到最后的解.
(2)首先利用绝对值三角不等式求得f的最小值,然后根据不等式的解集不是空集得到关于a的不等式,再解不等式即可.
4.已知a,b,c均为正实数.
(1)若ab+bc+ca=3,求证:a+b+c≥3.
(2)若a+b=1,求证:
▶ 解题指南
(1)要证明不等式成立,运用两边平方和不等式的性质,即可得到证明.
(2)运用分析法证明.要证a+b+c≥3,只需证明(a+b+c)2=a2+b2+c2+2ab+2bc+2ca≥9.
5.已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值.
(2)在第(1)问的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
▶ 解题指南
(1)不等式f(x)≤3就是|x-a|≤3,求出它的解集,与{x|-1≤x≤5}相同,求实数a的值.
(2)在第(1)问的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,根据f(x)+f(x+5)的最小值大于等于m,可求实数m的取值范围.
6.已知函数f(x)=m-|2-x|,且f(x+2)>0的解集为(-1,1).
(1)求m的值.
(2)若正实数a,b,c满足a+2b+3c=m,求![]() 的最小值.
的最小值.
▶ 解题指南
(1)由f(x+2)>0得|x|<m,求出解集,利用f(x+2)>0的解集(-1,1)求m的值.
(2)由(1)知,a+2b+3c=1,利用柯西不等式即可求![]() 的最小值.
的最小值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




