高考导航
1.理解函数单调性与导数的关系，考查利用分类讨论思想求函数单调性的能力，考查已知函数的单调性等条件逆向求参数范围.
2.了解函数在某点取得极值的必要条件和充分条件，理解导数的几何意义，会用导数求函数的极大值和极小值.
3.能够适当选取变量，建立函数模型，结合实际意义对问题进行探究，将问题与方程、不等式相结合，从而利用导数来解决问题.
4.考查运算能力、推理论证能力以及函数与方程思想、化归与转化的思想，体现了数学运算的核心素养.
例题精析
▶ 解题指南
能够掌握函数的对称轴或对称中心，观察原有函数的草图，感悟用数学语言表达和蕴含的数学思维.能够通过函数的奇偶性、周期性、对称性，来完成函数求解问题.
▶ 解析
因为f（x）是奇函数，得f（－x）＝－f（x），
所以f（1－x）＝－f（x－1）.
由f（1－x）＝f（1＋x），得－f（x－1）＝f（x＋1），
所以f（x＋2）＝－f（x），f（x＋4）＝－f（x＋2）＝－[－f（x）]＝f（x）.
故函数f（x）是周期为4的周期函数.由f（x）为奇函数，得f（0）＝0.
又因为f（1－x）＝f（1＋x），则f（x）的图像关于直线x＝1对称，所以f（2）＝f（0）＝0，f（－2）＝0.
又f（1）＝2，得f（－1）＝－2，
所以f（1）＋f（2）＋f（3）＋f（4）＝f（1）＋f（2）＋f（－1）＋f（0）＝2＋0－2＋0＝0，
故f（1）＋f（2）＋f（3）＋f（4）＋…＋f（49）＋f（50）
＝0×12＋f(49)＋f(50)＝f(1)＋f(2)＝2＋0＝2.
故选C.
变式2 1.已知函数f（x）是定义在R上的偶函数，且f（－x－1）＝f（x－1），当x∈[－1，0]时，f（x）＝－x3，则关于x的方程f（x）=|cos πx|在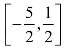
上的所有实数解之和为（ ）.
A.－7 B.－6 C.－3 D.－1
▶ 解析
函数f（x）是R上的偶函数，且f（－x－1）＝f（x－1），所以x＝－1是函数的对称轴，且周期为2，分别画出y＝f（x）与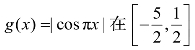
上的图像，如图7.1所示.
图7.1
交点依次为x1，x2，x3，x4，x5，x6，x7，得x1＋x7＝x2＋x6＝x3＋x5＝－2，x4＝－1，所以x1＋x2＋x3＋x4＋x5＋x6＋x7＝－2×3－1＝－7，故选A.
2.已知定义在R上的奇函数y＝f（x）满足f（2＋x）＝f（－x），且f（1）＝2，则f（2018）＋f（2019）的值为（ ）.
A.－2 B.0 C.2 D.4
▶ 解析
因为f（x）为奇函数，所以f（－x）＝－f（x）.
又f（2＋x）＝f（－x），则f（2＋x）＝－f（x），所以f（x＋4）＝－f（x＋2）＝f（x）.(www.xing528.com)
故函数f（x）是周期为4的周期函数.
所以f（2018）＋f（2019）＝f（4×504＋2）＋f（4×504＋3）＝f（2）＋f（3）.
又f（2）＝f（0）＝0，f（3）＝f（－1）＝－f（1）＝－2，
所以f（2018）＋f（2019）＝f（2）＋f（3）＝－2.
故选A.
【例3】（2015年高考新课标Ⅱ第12题）设函数f′（x）是奇函数f（x）（x∈R）的导函数，f（-1）=0当x＞0时，xf′（x）-f（x）＜0，则使得f（x）＞0成立的x的取值范围是（ ）.
A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)
C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)
▶ 解题指南
能够通过给出的求导数的形式，观察原有函数的模型，感悟用数学语言表达和蕴含的数学思维.能够通过求导讨论函数的单调性，来完成函数的零点与不等式的求解问题.
图7.2
▶ 解题指南
通过研究函数图像的方法，能够了解研究一个未知函数的研究方法和掌握规律性.以函数解析式为基础的函数图像问题，主要围绕函数解析式进行适当的化简后与一些熟知的函数图像联系，通过各种图像的变换得到所求函数的图像展开.有时利用函数的性质（如单调性、奇偶性、周期性等）来分析函数的图像特征从而判断函数图像.本题考查学生关于函数图像的基础知识和基本方法.
▶ 解析
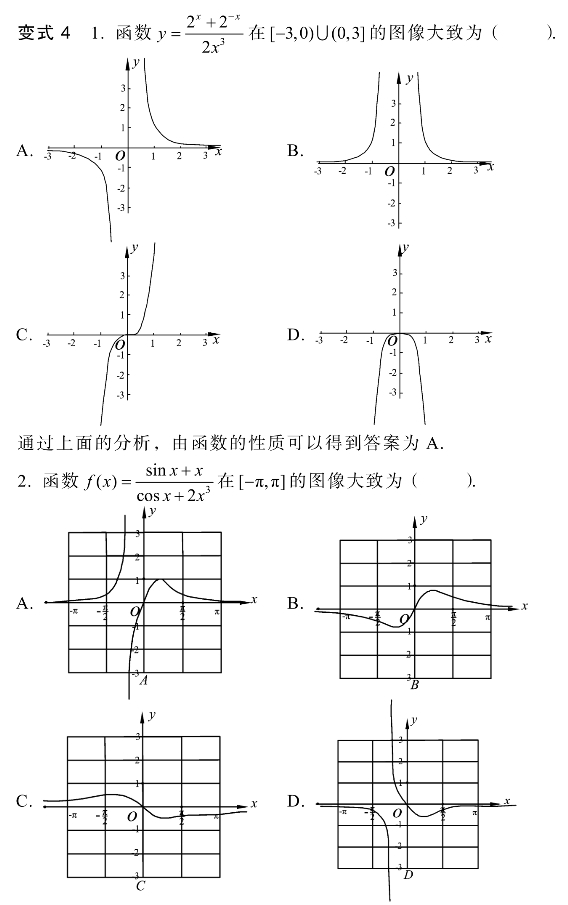
规范解答
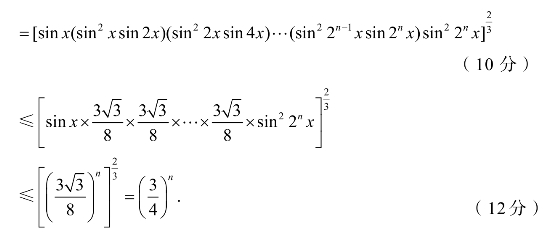
巩固提高
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
