高中数学高频考点：立体几何多解多变

高考导航

对立体几何的考查，全国Ⅲ卷4年8考，全国Ⅱ卷7年14考，全国Ⅰ卷8年15考，每年2题，一般考查三视图和球，主要是计算体积和表面积.其中，“点线面”也有可能出现在小题中，但是难度不大，立体几何是否会与其他知识点交汇？如几何概型（与体积有关的），有可能.但是，根据全国卷的命题习惯，交汇可能性不大.异面直线所成的角考了2次.球体是基本的几何体，是发展空间想象能力的很好载体，是新课标的热点.

2016年全国Ⅰ卷第11题考查了线线角，虽然没有提到异面直线，但是在发展空间想象能力和解题思路上与异面直线完全相同，2018年的第7题的考法体现了立体化为平面的思想法，2018年的第12题很好地考查了空间想象能力，也是作为压轴题出现.可以看出，全国卷不拘泥于在哪个知识点设计小题的压轴题，近年来三角、立体几何、数列都曾作为压轴题出现.

例题精析

【例1】（2019年全国I卷第12题）已知三棱锥P-ABC的四个顶点在球O的球面上，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，则球O的体积为（　　　　）.

▶　解题指南

（1）多面体外接球的定义.

（2）长方体外接球的半径（，其中a，b，c为长方体的棱长）.

（3）直棱柱外接球的半径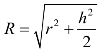（，其中r为底面多边形外接圆的半径，h为直棱柱的高）.

（4）方法：①直接法（定球心、定半径）；②补体法（将多面体补型为长方体或直棱柱模型）.

▶　解析

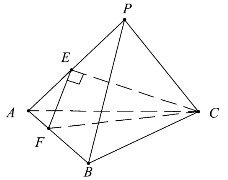
图4.1

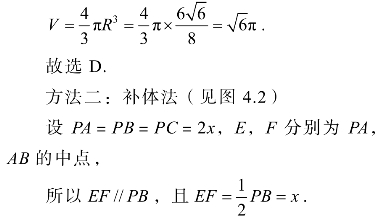
图4.2

2.已知三棱锥P-ABC（见图4.3）的四个顶点在球O的球面上，PA⊥平面ABC，PA＝4，底面△ABC是边长为3的等边三角形，则球O的表面积为______.

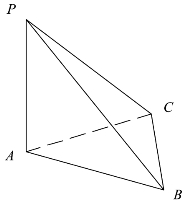
图4.3

▶　解析

3.四棱锥P-ABCD的三视图如图4.4所示，四棱锥P－AB CD的五个顶点都在一个球面上，E，F分别是棱AB，CD的中点，直线EF被球面所截得的线段长为，则该球的表面积为（　　　　）.

A.12π　　B.24π　　C.36π　　D.48π

图4.4

▶　解析

将三视图还原为直观图如图4.5所示，可得四棱锥P-ABCD的五个顶点位于同一个正方体的顶点处，且与该正方体内接于同一个球，且该正方体的棱长为a.

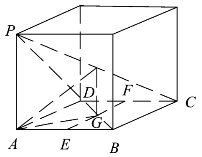
图4.5

设外接球的球心为O，则O也是正方体的中心，设EF的中点为G，连接OG，OA，AG.

根据题意，直线EF被球面所截得的线段长为，即正方体的面对角线长也是，可得，所以正方体的棱长a＝2，在Rt△OGA中，，即四棱锥P-ABCD的外接球半径，从而得外接球表面积为4πR2＝12π.

故选A.

【例2】已知△ABC的三个顶点都落在半径为R的球O的表面上，△ABC有一个角为且其对边长为3，球心O到△ABC所在平面的距离恰好等于半径R的一半，点P为球面上任意一点，则三棱锥P-ABC的体积的最大值为（　　　　）.

▶　解析

如图4.6所示，设△ABC外接圆的圆心为O1，则OO1⊥平面ABC，所以

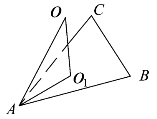
图4.6

变式2　1.如图4.7所示，四棱锥P-ABCD的底面为矩形，矩形的四个顶点A，B，C，D在球O的同一个大圆上，且球的表面积为16π，点P在球面上，则四棱锥P-ABCD体积的最大值为（　　　　）.

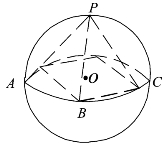
图4.7

▶　解析

因为球O的表面积是16π，所以S＝4πR2＝16π，解得R＝2.

设矩形的长、宽分别为x，y，则x2＋y2＝（2R）2≥2xy，当且仅当x＝y时等号成立.

即四棱锥P-ABCD的底面为正方形时，面积最大，此时

S正方形ABCD＝2R2＝8.

设四棱锥P-ABCD的高为h，当PO⊥底面ABCD时，hmax＝PO＝R，则四棱锥P-ABCD体积的最大值为

故选D.

2.已知三棱锥P-ABC（见图4.8）的四个顶点在球O的球面上，PA⊥平面ABC，PA＝6，，则球O的表面积为___________.

图4.8

【例3】已知三棱锥P-ABC（见图4.9）中，PA＝PB＝PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF＝90°，球O与三棱锥P-ABC的四个面均相切.则球O的体积为________.

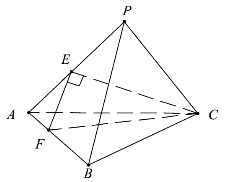
图4.9

▶　解题指南

（1）多面体内切球的定义.

（2）多面体内切球半径R与多面体体积的关系.

（3）方法：①直接法（定球心、定半径）；②等体积法.

如图4.10所示，设球O的半径为R.

图4.10

变式3　1.若圆锥的内切球与外接球的球心重合，且内切球的半径为1，则圆锥的体积为________.

▶　解析

过圆锥的旋转轴作轴截面，得截面△ABC及其内切圆⊙O1和外接圆⊙O2，且两圆同圆心，即△ABC的内心与外心重合，易得△ABC为正三角形.由题意知⊙O1的半径为r＝1，则△ABC的边长为，圆锥的底面半径为，高为3，故

答案：3π.

2.若一个正四面体的表面积为S1，其内切球的表面积为S2，则________.

▶　解析

【例4】（2018年北京高考卷理科）某四棱锥的三视图如图4.11所示，在此四棱锥的侧面中，直角三角形的个数为（　　　　）.

图4.11

A.1　　B.2　　C.3　　D.4

▶　解题指南

（1）三视图的概念及画法.

（2）基本几何体三视图的结构特点：①柱体；②椎体；③台体；④球体.

（3）三视图复原为直观图的技巧：借助长方体模型切割复原.注意：①方向感的训练；②虚实线的区别.

▶　解析

四棱锥的三视图对应的直观图如图4.12所示，PA⊥底面ABCD，，可得三角形PCD不是直角三角形.

(www.xing528.com)

图4.12

所以侧面中有3个直角三角形，分别为△PAB，△PBC，△PAD.

故选C.

变式4　某四棱锥的三视图如图4.13所示，则该四棱锥的最长棱的长度为（　　　　）.

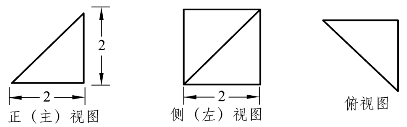
图4.13

▶　解析

四棱锥的三视图对应的直观图为S-ABCD，如图4.14所示，由已知SB⊥底面ABCD，SB＝AB＝BC＝CD＝DA＝2，，所以该四棱锥的最长棱的长度为

故选B.

图4.14

【例5】某三棱锥的三视图如图4.15所示，则该三棱锥的表面积是（　　　　）.

图4.15

▶　解析

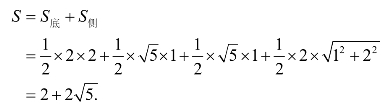
故选C.

【例6】（2019年全国Ⅱ卷理科）设α，β为两个平面，则α∥β的充要条件是（　　　　）.

A.α内有无数条直线与β平行

B.α内有两条相交直线与β平行

C.α，β平行于同一条直线

D.α，β垂直于同一平面

▶　解题指南

（1）熟记空间平行的有关性质.

（2）借助长方体模型进行分析.

▶　解析

A中，若无数条直线为无数条平行线，则无法得到α∥β，可知A错误；

B中，由两平面平行的判定定理知，α内两条相交直线都与β平行是α∥β的充分条件，由两平面平行性质定理知，α内两条相交直线都与β平行是α∥β的必要条件，即α内有两条相交直线与β平行是α∥β的充要条件；

C中，α，β平行于同一条直线，此时α与β可以相交，可知C错误；

D中，α，β垂直于同一平面，此时α与β可以相交，可知D错误.

故选B.

变式5　如图4.16所示的三棱柱ABC-A1B1C1中，侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC的中点，则下列叙述正确的是（　　　　）.

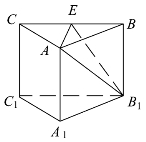
图4.16

A.CC1与B1E是异面直线

B.AC⊥平面ABB1A1

C.AE，B1C1为异面直线，且AE⊥B1C1

D.A1C1⊥平面AB1E

▶　解析

CC1，B1E是共面直线，故A错误；

若AC⊥平面ABB1A1，因为AB⊂平面ABB1A1，故AC⊥AB，这与矛盾，故B错误；

由AC＝AB，CE＝EB，可以得到AE⊥BC，又BC∥B1C1，故AE⊥B1C1，又由AE∩平面B1BCC1＝E，B1C1⊂平面B1BCC1，E∉B1C1，故AE，B1C1是异面直线，故C正确；

若A1C1⊥平面AB1E，因为AB1⊂平面AB1E，故A1C1⊥AB1，因为AA1⊥平面A1B1C1，A1C1⊂平面A1B1C1，故A1C1⊥AA1，而A1A∩AB1＝A，故A1C1⊥平面AA1B1B，又A1B1⊂平面AA1B1B，故A1C1⊥A1B1，这与矛盾，故D错误.

故选C.

巩固提高

1.（2012年全国卷）已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此三棱锥的体积为（　　　　）.

2.某圆锥的母线长为2，高为，其三视图如图4.17所示.圆锥表面上的点M在正（主）视图上的对应点为A，圆锥表面上的点N在侧（左）视图上的对应点为B，则在此圆锥侧面上，从M到N的路径中，最短路径的长度为（　　　　）.

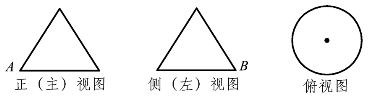
图4.17

3.某几何体的三视图如图4.18所示，则该几何体的外接球的表面积为（　　　　）.

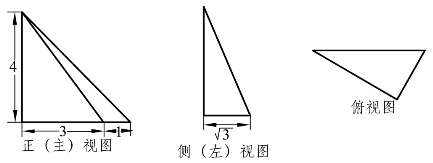
图4.18

A.25π　　B.26π　　C.32π　　D.36π

4.已知一个圆锥底面半径为1，母线长为3，则该圆锥内切球的表面积为（　　　　）.

5.设m，n表示不同直线，α，β表示不同平面，则下列结论中正确的是（　　　　）.

A.若m∥α，m∥n，则n∥α

B.若m⊂α，n⊂β，m∥β，n∥α，则α∥β

C.若α∥β，m∥α，m∥n，则n∥β

D.若α∥β，m∥α，n∥m，n⊄β，则n∥β

6.有以下三种说法，其中正确的是（　　　　）.

① 若直线a与平面α相交，则α内不存在与a平行的直线；

② 若直线b∥平面α，直线a与直线b垂直，则直线a不可能与α平行；

③ 直线a，b满足a∥b，则a平行于经过b的任何平面.

A.①②　　B.①③　　C.②③　　D.①

7.如图4.19所示，平面α与平面β相交于BC，AB⊂α，CD⊂β，点A∉BC，点D∉BC，则下列叙述错误的是（　　　　）.

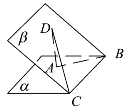
图4.19

A.直线AD与BC是异面直线

B.过AD只能作一个平面与BC平行

C.过AD只能作一个平面与BC垂直

D.过D只能作唯一平面与BC垂直，但过D可作无数个平面与BC平行

8.如图4.20所示，网格纸上小正方形的边长为1，粗线表示的是某几何体的三视图，则该几何体外接球的表面积为（　　　　）.

图4.20

A.24π　　B.29π　　C.48π　　D.58π

9.如图4.21所示，网格纸上小正方形的边长为a，粗实线画出的是某几何体的三视图，若该几何体的表面积为，则a的值为（　　　　）.

图4.21

10.如图4.22所示的是某几何体的三视图，则该几何体的外接球的表面积为（　　　　）.

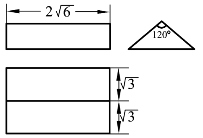
图4.22

A.24π　　B.36π　　C.40π　　D.400π

11.一个几何体的三视图如图4.23所示，则这个几何体的体积为（　　　　）.

图4.23

12.已知H是球O的直径AB上一点，AH∶HB＝1∶2，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为（　　　　）.