高中数学高频考点：概率统计

高考导航

1.古典概型、几何概型，多以选择题或填空题的形式命题，题目难度一般属于中低档.

2.概率模型多考查独立重复实验、相互独立事件、互斥事件及对立事件等，对离散型随机变量的分布列及期望的考查是重点中的“热点”，多在解答题的前三题的位置呈现.常考查相互独立事件的概率、超几何分布和二项分布的期望等.

例题精析

【例1】某商场举行有奖促销活动，抽奖规则如下：箱子中有编号为1，2，3，4，5的五个形状、大小完全相同的小球，从中任取两球，若摸出的两球号码的乘积为奇数，则中奖；否则不中奖.中奖的概率为（　　　　）.

▶　解题指南

利用古典概型公式，m是事件A包含的基本事件数，n是基本事件总数，求古典概型的概率，关键是正确求出基本事件总数和所求事件包含的基本事件总数.常常用到排列、组合的有关知识，计数时要正确分类，做到不重不漏.

▶　解析

从五个球中任取两球有种情况，其中两球编号的乘积为奇数的有故选C.

变式1　某商场举行有奖促销活动，抽奖规则如下：箱子中有编号为种情况，所以所求事件的概率1，2，3，4，5的五个形状、大小完全相同的小球，从中任取两球，若摸出的两球号码的和为奇数，则中奖；否则不中奖.中奖的概率为（　　　　）.

▶　解析

从五个球中任取两球有种情况，其中两球编号的和为奇数的有6种情况，所以所求事件的概率故选D.

【例2】太极图是以黑白两个鱼形纹组成的图形图案，它形象化地表达了阴阳轮转、相反相成是万物生成变化根源的哲理，展现了一种相互转化、相对统一的形式美.按照太极图的构图方法，在平面直角坐标系中，圆O被的图象分割为两个对称的鱼形图案（如图3.1所示）.其中小圆的半径均为1，现在大圆内随机取一点，则此点取自阴影部分的概率为________.

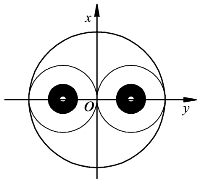
图3.1

▶　解题指南

此题属于几何概型问题.在计算几何概型的概率时，寻找构成试验的全部结果的区域和事件发生的区域是关键，有时涉及函数问题，需要借助函数的性质得出所求面积.

▶　解析

变式2　1.太极图是以黑白两个鱼形纹组成的图形图案，它形象化地表达了阴阳轮转相反相成是万物生成变化根源的哲理，展现了一种相互转化、相对统一的形式美.按照太极图的构图方法，在平面直角坐标系中，圆O被y＝2sin ωx的图像分割为两个对称的鱼形图案（如图3.1所示）.其中小圆的半径均为1，现在大圆内随机取一点，且此点取自阴影部分的概率为，则ω=________.

▶　解题指南

考查几何概型中的面积比，主要是求阴影部分的面积，注意涉及的三角函数知识.

▶　解析

2.三国时期吴国的数学家赵爽曾创制了一幅“勾股圆方图”，用数形结合的方法给出了勾股定理的详细证明.如图3.2所示的“勾股圆方图”中，四个全等的直角三角形与中间的小正方形拼成一个大正方形，其中一个直角三角形中较小的锐角α满足，现向大正方形内随机投掷一枚飞镖，则飞镖落在小正方形内的概率是（　　　　）.

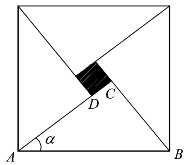
图3.2

【例3】（2016年全国Ⅱ卷）某险种的基本保费为a（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：

设该险种一续保人一年内出险次数与相应概率如下：

（1）求一续保人本年度的保费高于基本保费的概率.

（2）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率.

▶　解题指南

求随机事件的概率，要正确分析随机事件的构成，看随机事件是否能转化为几个彼此互斥的事件的和事件，特别注意是否为条件概率.

▶　解析

（1）设A表示事件：“一续保人本年度的保费高于基本保费”，则事件A发生当且仅当一年内出险次数大于1，故

P（A）＝0.20＋0.20＋0.10＋0.05＝0.55.

（2）设B表示事件：“一续保人本年度的保费比基本保费高出60%”，则事件B发生当且仅当一年内出险次数大于3，故

P（B）＝0.10＋0.05＝0.15.

又P（AB）＝P（B），故

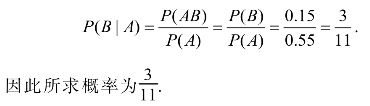
变式3　其余条件不变，将第二个表格改为

且m=4n.

（1）求m，n的值.

（2）求续保人本年度保费的均值.

▶　解题指南

首先分清基本事件，正确理解每一个取值对应的概率之和为1，求均值即求数学期望.

▶　解析

（1）因为m=4n，m+n=0.25，解得m=0.2，n=0.05.

（2）均值即期望，设续保人本年度保费为X，其分布列为

则

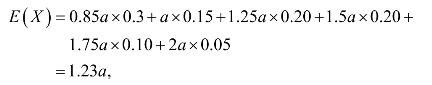
即续保人本年度保费的均值为1.23a.

【例4】多家央企为了配合国家战略支持雄安新区建设，纷纷申请在新区建立分公司.若规定每家央企只能在雄县、容城、安新3个片区中的1个片区设立分公司，且申请其中任一个片区设立分公司都是等可能的，每家央企选择哪个片区相互之间互不影响且必须在其中一个片区建立分公司.向雄安新区申请建立分公司的任意4家央企中.

（1）求恰有2家央企申请在“雄县”片区建立分公司的概率.

（2）用X表示这4家央企中在“雄县”片区建立分公司的个数，用Y表示在“容城”或“安新”片区建立分公司的个数，记ξ＝|X－Y|，求ξ的分布列.

变式4　1.随着社会的发展，人们在购买商品时支付的方式呈现多样化.某超市在顾客支付商品时可提供现金支付、信用卡支付、微信支付三种支付方式.超市统计结果显示，用“现金支付”的人约占，用“信用卡支付”的人约占，用“微信支付”的人约占.若用上面的频率表示概率，现有甲、乙、丙三人，他们选择支付的方式互不影响.

（1）求三人选择支付方式互不相同的概率.

（2）在甲、乙选择的支付方式相同的条件下，X表示甲、乙、丙三人选择微信支付的人数，求X的分布列与期望.

▶　解题指南

（1）根据计数原理及相互独立事件的概率乘法公式，可以得出结论.

（2）先求出甲、乙选择的支付方式相同的条件下选择微信支付的概率，和甲、乙选择的支付方式相同的条件下不选择微信支付的概率，列出随机变量X的所有可能的取值，求出对应的概率，列出分布列，求期望即可.

▶　解析

（1）三人选择支付方式互不相同的概率为

（2）因为甲、乙选择的支付方式相同，所以甲、乙选择微信支付的概率为

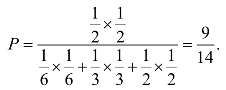
故甲、乙不选择微信支付的概率为5/14.

由已知，可得X的可能取值为0，1，2，3，得

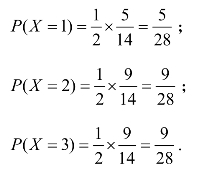
则X的分布列为

2.为响应国家“精准扶贫，产业扶贫”战略的号召，进一步优化能源消费结构，某市决定在地处山区的A县推进光伏发电项目.在该县山区居民中随机抽取50户，统计其年用电量得出以下统计表.以样本的频率作为概率.

（1）在该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数为X，求X的数学期望.

（2）已知该县某山区自然村有居民300户.若计划在该村安装总装机容量为300千瓦的光伏发电机组，该机组所发电量除保证该村正常用电外，剩余电量国家电网以0.8元/度的价格进行收购.经测算每千瓦装机容量的发电机组年平均发电1 000度，试估计该机组每年所发电量除保证正常用电外还能为该村创造直接收益多少元.

▶　解题指南

主要考查用样本估计总体.

（1）根据样本得到事件A发生的概率，且X服从二项分布，由二项分布的期望公式可得X的期望.

（2）根据样本求得该县山区居民户年均用电量，即每户年用电量的期望，从而可得该县居民用电总量，即可得直接收益.

▶　解析

（1）记在抽取的50户居民中随机抽取1户，其年用电量不超过600度为事件A，则

由已知可得，从该县山区居民中随机抽取10户，记其中年用电量不超过600度的户数为X，且，故

（2）设该县山区居民户年均用电量为E（Y），由抽样可得

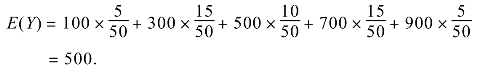
则该自然村年均用电约150 000度.又该村所装发电机组年预计发电量为300 000度，故该机组每年所发电量除保证正常用电外还能剩余电量约150 000度，能为该村创造直接收益150 000×0.8＝120 000元.

【例5】（2017年全国Ⅲ卷）某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶作降价处理，以每瓶2元的价格当天全部处理完.根据往年销售经验，每天需求量与当天最高气温（单位：°C）有关.如果最高气温不低于25 °C，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20 °C，需求量为200瓶.为了确定6月份的订购计划，统计了前三年6月份各天的最高气温数据，得下面的频数分布表.

以最高气温位于各区间的频率估计最高气温位于该区间的概率.

（1）求6月份这种酸奶一天的需求量X（单位：瓶）的分布列.

（2）设6月份一天销售这种酸奶的利润为Y（单位：元），当6月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？

▶　解题指南(www.xing528.com)

（1）求离散型随机变量的分布列，确定随机变量的取值是关键，然后求出每一个可能值的概率，列出随机变量的分布列.

（2）根据题目所要解决的问题，确定自变量及其取值范围；确定利润Y与进货量的函数关系；求出利润的数学期望E（Y）与进货量n的关系；利用函数的性质，求E（Y）的最大值.

▶　解析

（1）由题意知，X所有的可能取值为200，300，500.

由表格数据知，

P(X=200)=0.2；

P(X=300)=0.4；

P(X=500)=0.4.

则X的分布列为

（2）由题意知，这种酸奶一天的需求量至多为500瓶，至少为200瓶，因此只需考虑200≤n≤500.

当300≤n≤500时，

若最高气温不低于25 °C，则Y＝6n－4n＝2n；

若最高气温位于区间[20，25），则Y＝6×300＋2（n－300）－4n＝1 200－2n；

若最高气温低于20 °C，则Y＝6×200＋2（n－200）－4n＝800－2n，因此

E(Y)＝2n×0.4＋(1 200－2n)×0.4＋(800－2n)×0.2＝640－0.4n.

当200≤n＜300时，

若最高气温不低于20 °C，则Y＝6n－4n＝2n；

若最高气温低于20 °C，则Y＝6×200＋2（n－200）－4n＝800－2n，因此

E(Y)＝2n×(0.4＋0.4)＋(800－2n)×0.2＝160＋1.2n.

故n＝300时，Y的数学期望达到最大值，最大值为520元.

变式5　1.某生鲜超市每天从蔬菜生产基地购进某种蔬菜，每天的进货量相同，进价6元/千克，售价9元/千克，当天未售出的蔬菜被生产基地以2元/千克的价格回收处理.该超市发现这种蔬菜每天都有剩余，为此整理了过往30天这种蔬菜的日需求量X（单位：千克），得到如下统计数据：

以这30天记录的各日需求量的频率作为各日需求量的概率，假设各日需求量相互独立.

（1）求在未来的3天中，至多有1天的日需求量不超过190千克的概率.

（2）超市为了减少浪费，提升利润，决定调整每天的进货量n（单位：千克），以销售这种蔬菜的日利润的期望值为决策依据，在n＝180与n＝200之中选其一，应选用哪个？

▶　解题指南

（1）注意辨别独立重复试验的基本特征：①在每次试验中，试验结果只有发生与不发生两种情况；②在每次试验中，事件发生的概率相同.

（2）牢记公式，k＝0，1，2，…，n，并深刻理解其含义.

▶　解析

（1）依题意，日需求量不超过190的概率为

记“未来的3天中，至多有1天的日需求量不超过190”为事件A，则

（2）设日利润为Y元.

① 当n＝180时，

若X＝160，则Y＝160×3－20×4＝400；

若X＝170，则Y＝170×3－10×4＝470；

若X≥180，则Y＝180×3＝540.

则Y的分布列为

② 当n＝200时，

若X＝160，则Y＝160×3－40×4＝320；

若X＝170，则Y＝170×3－30×4＝390；

若X＝180，则Y＝180×3－20×4＝460；

若X＝190，则Y＝190×3－10×4＝530；

若X≥200，则Y＝200×3＝600.

则Y的分布列为

（1）若A水果日需求量为140千克，则

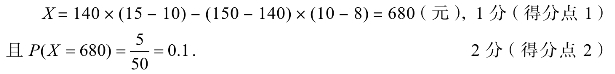
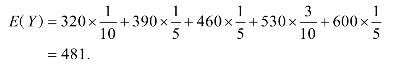
故当n＝180时日利润的期望值大于当n＝200时日利润的期望值，应选n＝180.

规范解答

1.某大型水果超市每天以10元/千克的价格从水果基地购进若干A水果，然后以15元/千克的价格出售，若有剩余，则将剩余的水果以8元/千克的价格退回水果基地，为了确定进货数量，该超市记录了A水果最近50天的日需求量（单位：千克），整理得到下表.

以50天记录的各日需求量的频率代替各日需求量的概率.

（1）若该超市一天购进A水果150千克，记超市当天A水果获得的利润为X（单位：元），求X的分布列及其数学期望.

（2）若该超市计划一天购进A水果150千克或160千克，请以当天A水果获得的利润的期望值为决策依据，在150千克与160千克之中选其一，应选哪一个？若受市场影响，剩余的水果以7元/千克的价格退回水果基地，又该选哪一个？

▶　解析（满分解答）

若A水果日需求量不小于150千克，则

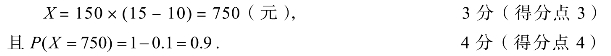
故X的分布列为

（2）设该超市一天购进A水果160千克，当天的利润为Y（单位：元），则Y的可能取值为

140×5－20×2，150×5－10×2，160×5，即660，730，800.

故Y的分布列为

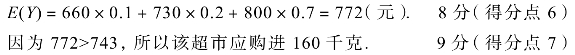
若剩余的水果以7元/千克的价格退回水果基地，同理可得X，Y的分布列分别为

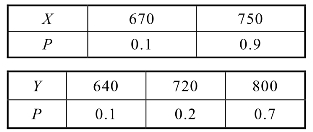
巩固提高

1.甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为a，再由乙猜甲刚才所想的数字，把乙猜的数字记为b，其中a，b∈{1，2，3，4，5，6}，若|a -b|≤1，就称甲、乙“心有灵犀”.现任意找两人玩这个游戏，则他们“心有灵犀”的概率为（　　　　）.

2.《周髀算经》记载了勾股定理的公式和证明，图3.3是与勾股定理有关的图形，它由三个正方形和一个直角三角形组成.若图中a，b，c的值分别为3，4，5，则在图中任取一点P，该点取自阴影部分的概率为（　　　　）.

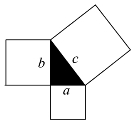
图3.3

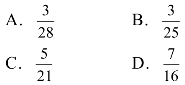
3.如图3.4所示，在面积为S的△ABC的边AB上任取一点P，则△PBC的面积大于的概率是（　　　　）.

图3.4

4.服用某种新药后每位病人被治愈的概率均为0.9，服用这种新药的有甲、乙、丙3位病人，且各人之间互不影响，下列结论中错误的是（　　　　）.

A.3位病人都被治愈的概率为0.93

B.3人中恰好有2人被治愈的概率是3×0.92×0.1

C.3人中恰好有2人未被治愈的概率是3×0.9×0.12

D.3人中恰好有2人被治愈，且甲被治愈的概率是0.92×0.1

5.从1，2，3，4，5，6，7，8，9中不放回地依次取2个数，事件A＝“第一次取到的是奇数”，事件B＝“第二次取到的是奇数”，则P（B |A）=________.

6.在区间[0，1]上随意选择两个实数x，y，则使成立的概率为________.

7.已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分.现从该箱中任取（无放回，且每球取到的机会均等）3个球，记随机变量X为取出3球所得分数之和.

（1）求X的分布列.

（2）求X的数学期望E（X）.

8.手机行业的快速发展，方便了人们的生活，同时也给人们带来了痛苦.某理疗室医生对前来理疗的50人进行问卷调查，统计得到了如下数据：

将看手机时间在[4，8]内定义为“长时间看手机”，看手机时间在[0，4）内定义为“不长时间看手机”.

（1）请将下面的列表补充完整：

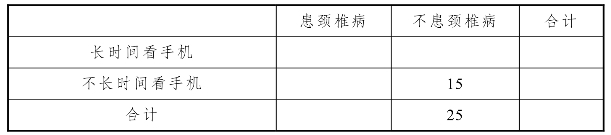
（2）是否有99.9%的把握认为长时间看手机与患颈椎病有关？说明你的理由.

（3）将上述调查所得的频率视为概率，现在从大量的理疗患者中，采用随机抽样的方法每次抽取1名，抽取2次，记被抽取的2人中的“长时间看手机”人数为X.若每次抽取的结果是相互独立的，求X的分布列及数学期望E（X）和方差D（X）.

参考：