假设检验基本步骤及选择方法

（一）假设检验的基本步骤

假设检验又称显著性检验，是统计推断的重要内容之一。假设检验的基本原理是先对总体参数或分布作出假设，再选用适当的统计方法，利用样本提供的信息，检验刚才提出的假设成立的概率，再依据“小概率事件”原理，决定是否拒绝该假设。

例7．17　已知正常成年男性的脉搏均数为72．0次／分。在调查中某科室随机抽取25名同种疾病患者，测得其脉搏均数为74．2次／分，标准差为6．5次／分。试问该疾病患者的脉搏均数与一般健康成年男性的脉搏均数是否不同？

从上例中可以看出样本均数与总体均数之间存在差异。如何判断差异出现的原因？这就需要进行假设检验，基本步骤如下：

1．建立检验假设，确定检验水准

（1）建立检验假设，包括两方面：

1）无效假设H0：H0表示上例中该疾病患者的脉搏均数μ与一般健康成年男性的脉搏均数μ0相等，即μ＝μ0，两总体均数相等，差异是由于抽样误差形成的。

2）备择假设H1：H1表示上例中该疾病患者的脉搏均数μ与一般健康成年男性的脉搏均数μ0不等，即μ≠μ0，两总体均数不相等，差异不是由于抽样误差形成的。

在假设检验中，H0是主要的，只有拒绝了H0，才能接受H1。

（2）确定检验水准：检验水准是预先规定的小概率事件的标准，用α表示。它是“是否拒绝H0的界限”。研究者可以根据研究目的规定α的大小，通常α取0．05。

2．选择检验方法，计算统计量　要根据统计推断的目的、研究设计的类型和样本量的大小等条件，选用合适的检验方法和计算相应的统计量。

3．确定P值，作出推断结论　P值是指从H0所规定的总体中做随机抽样，获得等于及大于（或等于及小于）现有样本的检验统计量值（如t值或z值）的概率。

将概率P与检验水准α比较，然后作出推断：

当P≤α时，则拒绝H0，接受H1，差异有统计学意义；当P＞α时，尚不能拒绝H0，差异无统计学意义。

（二）均数的t检验

适用于样本含量n较小时，理论上要求样本来自正态分布的总体。

1．样本均数与已知总体均数比较的t检验　又称单样本t检验。“已知总体均数”一般为理论值、标准值或经过大量观察所得到的稳定值等。已知总体均数为μ0，样本均数所代表的未知总体均数为μ，假设检验的目的：推断这两者是否相等。如例7．17，假设检验过程如下：

（1）建立检验假设，确定检验水准

H0：μ＝μ0，该疾病患者的脉搏均数与一般健康成年男性的脉搏均数相等；

H1：μ≠μ0，该疾病患者的脉搏均数与一般健康成年男性的脉搏均数不等；

α＝0．05。

（2）选择检验方法，计算统计量

代入例7．10中数值，计算t值。

（3）确定P值，作出推断结论

在例7．10中自由度υ＝25－1＝24，查t界值表得出t0．05，24＝2．064，在第（2）步中得到t＝1．69＜2．064，因此P＞0．05，按照α＝0．05的检验水准，不拒绝H0，差异无统计学意义。

2．配对设计资料的t检验　配对设计是将受试对象按可能会影响研究结果的某些特征或属性相近的原则配对。每对中的两个个体随机地给予两种处理，若两种处理的效应相同或某种处理没发生作用，两总体均数相等，即μ1＝μ2，即差值的总体均数μd＝0。配对设计的t检验是计算样本差值均数与已知差值的总体均数0的比较。计算公式是：

式中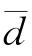为差值的样本均数；sd为差值的标准差；n为对子数。

例7．18　使用某新型高血压治疗的患者10名，记录这些患者治疗前后舒张压（mmHg）的变化，见表7－5。试推断该新药对高血压患者的舒张压变化是否有影响。

表7－5　高血压患者治疗前后舒张压（mmHg）测量结果

（1）建立检验假设，确定检验水准

H0：μd＝0，该新药对高血压患者舒张压的变化无影响；

H1：μd≠0，该新药对高血压患者舒张压的变化有影响；

α＝0．05。

（2）选择检验方法，计算统计量

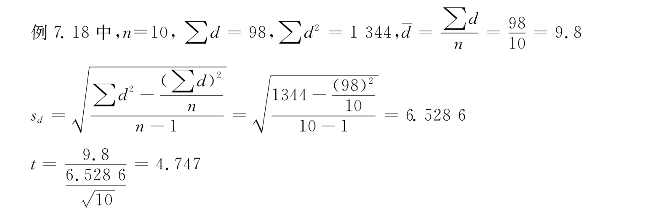
（3）确定P值，作出推断结论

按照υ＝10－1＝9，查t界值表，得出双侧界值t0．05／2，9＝2．262，t0．001／2，9＝4．781，因此t＞t0．05／2，9，则P＜0．05，按照α＝0．05的检验水准，拒绝H0，接受H1，差异有统计学意义。可以推断该新药对高血压患者的舒张压有影响，治疗之后可使得患者舒张压降低。

3．两独立样本资料的t检验　适用于完全随机设计的资料，推断两样本均数所代表的总体均数是否相同。计算公式是：

式中，X1和X2为两样本均数，s 1－ 2为两样本均数之差的标准误，计算公式是：

例7．19　观察某新药对急性黄疸型肝炎的退黄效果，与单独使用输液法保肝的病人对照观察，两组患者黄疸指数在30～50（mg／dl），每个人的退黄天数如下，推断新药组（1组）与对照组（2组）退黄天数有无差别。

新药组（天）：5 7 8 10 11

对照组（天）：15 18 16 20 21

（1）建立检验假设，确定检验水准

H0：μ1＝μ2，该新药对缩短退黄天数无影响；

H1：μ1≠μ2，该新药对缩短退黄天数有影响；

α＝0．05。

（2）选择检验方法，计算统计量

（3）确定P值，作出推断结论

按照υ＝8，α＝0．05，查t界值表，得出t0．05，8＝2．306。因为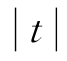＞t0．05，8，所以，P＜0．05，按照α＝0．05的检验水准，拒绝H0，接受H1，两组退黄天数差异有统计学意义。可以推断该新药对急性黄疸型肝炎患者的退黄天数有影响，治疗之后可使得患者退黄天数缩短。

（三）z检验

当样本含量较大时，样本均数近似正态分布，可用z检验。统计量z的计算公式为：

例7．20　某医院对50～65岁年龄组的不同性别的健康人群进行白细胞数（109／L）调查，结果见表7－6。试推断不同性别健康人群的白细胞数有无差别。

表7－6　健康成人白细胞数（109／L）测得值

（1）建立检验假设，确定检验水准

H0：不同性别健康人群的白细胞数无差异；

H1：不同性别健康人群的白细胞数有差异；

α＝0．05。

（2）选择检验方法，计算统计量

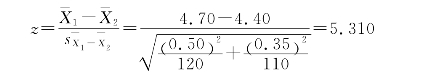
（3）确定P值，作出推断结论

本题中统计量z＝5．310＞z0．01＝2．58，P＜0．01，按照α＝0．05的检验水准，拒绝H0，接受H1，差异有统计学意义。可以推断健康人群的白细胞数有性别差异，男性白细胞均数高于女性。

（四）t检验应用时应注意的问题

1．要有严密的研究设计　这是假设检验的前提。组间应均衡，具有可比性，也就是除对比的主要因素（如临床试验用新药和对照药）外，其他可能影响结果的因素（如年龄、性别、病程、病情轻重等）在对比组间应相同或相近。保证均衡性的方法主要是从同质总体中随机抽取样本，或随机分配样本。(www.xing528.com)

2．不同的资料应选用不同检验方法　应根据分析目的、资料类型以及分布、设计方案的种类、样本含量大小等选用适当的检验方法。如：配对设计的计量资料采用配对t检验。而完全随机设计的两样本计量资料，若为小样本且方差齐，则选用两样本t检验；若方差不齐，则选用近似t检验。

3．正确理解“显著性”一词的含义　差别有或无统计学意义，过去称差别有或无“显著性”，是对样本统计量与总体参数或样本统计量之间的比较而言，相应推断为：可以认为或还不能认为两个或多个总体参数有差别。

4．结论不能绝对化　因统计结论具有概率性质，故“肯定”、“一定”、“必定”等词不要使用。在报告结论时，最好列出检验统计量的值，尽量写出具体的P值或P值的确切范围，如写成P＝0．040或0．02＜P＜0．05，而不简单写成P＜0．05，以便读者与同类研究进行比较。

5．结论与专业结合　假设检验是为专业服务的，统计结论必须和专业结论有机地相结合，才能得出恰如其分、符合客观实际的最终结论。若统计结论和专业结论一致，则最终结论就和这两者均一致（即均有或均无意义）；若统计结论和专业结论不一致，则最终结论需根据实际情况加以考虑。若统计结论有意义，而专业结论无意义，则可能由于样本含量过大或设计存在问题，那么最终结论就没有意义。例如：有人欲比较A、B两种降压药物的降压效果，随机抽取了高血压病人各100名，分别测定两组病人服药后舒张压的改变值，得两组舒张压改变值之差的平均数为0．83mmHg（0．11kPa）。做两独立样本资料的t检验，得t＝6．306，P＜0．001，有统计学意义。但因A、B两组高血压病人服药后舒张压改变值之差较小，仅0．83mmHg，未达到有临床意义的差值5mmHg（0．67kPa），故最终结论没有意义。相反，若统计结论无意义，而专业结论有意义，那就应当检查设计是否合理、样本含量是否足够。

（苏　英）

一、名词解释

1．算术均数　2．中位数　3．百分位数　4．标准差　5．变异系数　6．标准误　7．可信区间　8．假设检验

二、选择题

1．描述计量资料的主要统计指标是　（　）

A．平均数　B．相对数　C．t值　D．标准误　E．概率

2．一群7岁男孩身高标准差为5cm，体重标准差为3kg，则二者变异程度比较　（　）

A．身高变异大于体重　B．身高变异小于体重

C．身高变异等于体重　D．无法比较

E．身高变异不等于体重

3．随机抽取某市12名男孩，测得其体重均值为3．2kg，标准差为0．5kg，则总体均数95%可信区间的公式是　（　）

4．以下指标中哪一项可用来描述计量资料离散程度　（　）

A．算术均数　B．几何均数　C．中位数　D．极差　E．第50百分位数

5．偏态分布资料宜用下面哪一项描述其分布的集中趋势　（　）

A．算术均数　B．标准差　C．中位数　D．四分位数间距　E．方差

6．正态曲线下、横轴上，从均数到＋∞的面积为　（　）

A．97．5%　B．95%　C．50%　D．5%　E．不能确定

7．下面哪一项分布的资料，均数等于中位数　（　）

A．对数正态　B．左偏态　C．右偏态　D．偏态　E．正态

8．对于正态分布资料的95%正常值范围，宜选用　（　）

9．做频数表时，以组距为5，下列哪项组段划分正确　（　）

A．0～，5～，10～，…　B．0～5，5～10，10～，…

C．～5，～10，～15，…　D．0～4，5～9，10～，…

E．5～，7～，9～，…

10．均数与标准差之间的关系是　（　）

A．标准差越小，均数代表性越大　B．标准差越小，均数代表性越小

C．均数越大，标准差越小　D．均数越大，标准差越大

E．标准差越大，均数代表性越大

11．15名妇女分别用两种测量肺活量的仪器测最大呼气率（L／min），比较两种方法检测结果有无差别，可进行　（　）

A．单样本t检验　B．成组设计t检验　C．单因素方差分析

D．配对设计t检验　E．卡方检验

12．比较两种药物疗效时，对于下列哪项可作单侧检验　（　）

A．已知A药与B药均有效　B．不知A药好还是B药好

C．已知A药不会优于B药　D．不知A药与B药是否均有效

E．已知A药与B药均无效

13．配对t检验中，用药前数据减去用药后数据和用药后数据减去用药前数据，两次t检验的结果（　）

A．t值符号相反，结论相反　B．t值符号相同，结论相同

C．t值符号相反，但结论相同　D．t值符号相同，但大小不同，结论相反

E．t值符号与结论无关

14．下面哪一项小，表示用该样本均数估计总体均数的可靠性大　（　）

A．CV　B．s　C．s D．R　E．四分位数间距

15．两个小样本数值变量资料比较的假设，首先应考虑　（　）

A．t检验　B．u检验　C．秩和检验

D．t检验和秩和检验均可　E．资料符合t检验还是秩和检验

16．抽样误差是指　（　）

A．总体参数与总体参数间的差异　B．个体值与样本统计量间的差异

C．总体参数间的差异　D．样本统计量与总体统计量间的差异

E．以上都不对

17．统计推断的内容　（　）

A．是用样本指标估计相应的总体指标　B．是检验统计上的“假设”

C．a、b均不是　D．a、b均是

E．以上都错

18．两样本均数比较，经t检验，差别有显著性时，P越小，说明　（　）

A．两样本均数差别越大　B．两总体均数差别越大

C．越有理由认为两总体均数不同　D．越有理由认为两样本均数不同

E．样本均数与总体均数不同

19．表示均数的抽样误差大小的统计指标是　（　）

A．标准差　B．方差　C．均数标准误　D．变异系数　E．极差

三、计算题

1．大量研究显示，汉族足月正常产男性新生儿临产前双顶径均数为9．3cm。某医生记录了某山区12名汉族足月正常产男性新生 儿临产前双顶径（cm）资料：9．95，9．33，9．49，9．00，10．09，9．15，9．52，9．33，9．16，9．37，9．11，9．27。

试问该山区男性新生儿临产前双顶径是否与一般新生儿相等？

2．某地抽样调查了36名健康成年男性的红细胞数，其均数为4．66，标准差为0．58，同时调查女性红细胞均数为4．35，标准差为4．84，问男女有无差别？

3．研究者为比较耳垂血和手指血的白细胞数，调查8名成年人，同时采取耳垂血和手指血，资料如下：

若资料服从正态分布，试比较两者的白细胞数是否相同。