集中趋势指标：预防医学中的平均数、中位数和几何均数

集中趋势是代表一组同质变量值的集中位置或平均水平，用平均数表示。医学上常用的平均数有算术均数、几何均数和中位数。

（一）算术均数

算术均数简称均数，主要适用于描述对称分布资料，尤其适合呈正态分布或近似正态分布的资料。一般以希腊字母μ表示总体均数，以X—表示样本均数。其计算方法有以下两种。

1．直接法　当观察值例数较少时，可以将各观察值相加，再除以观察值的例数，计算公式是：

公式中，X1、X2、…、Xn表示观察值；n表示样本含量；Σ表示求和符号。

例7．2　测得10名正常成年男性的脉搏（次／分）分别是82，77，79，80，68，75，69，80，72，74，求脉搏均数。

即10名正常成年男性的脉搏均数为75．6次／分。

2．加权法　当资料中观察值个数较多时，用直接方法计算比较繁琐，宜改用加权法计算其均数。公式如下：

式中，R为组段数，i＝1，2，3…R，fi为各组段的频数，xi为组中值，Σfi＝n。

例7．3　某地101例健康男子血清总胆固醇值（mmol／L）见表7－2，求其平均值。

表7－2　某地101例健康男子血清总胆固醇值（mmol／L）均数及标准差计算表

即该地101例健康男子血清总胆固醇平均值为4．21mmol／L。

（二）几何均数

几何均数简记为G，适用于变量值呈倍数关系或呈对数正态分布（正偏态分布）的资料，如抗体效价及抗体滴度，某些传染病的潜伏期细菌计数等。计算公式为：

1．直接法　当观察值个数较少时，可以用公式7－3或7－4直接计算。

例7．4 5人的血清中某抗体效价分别为：1∶20、1∶16、1∶32、1∶40、1∶32，求平均效价。

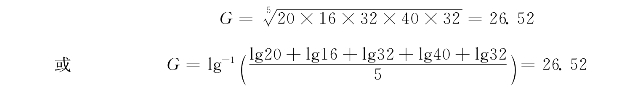
即该资料的平均效价为1∶26．52。

2．加权法　当资料中观察值个数较多时，可以先编制成频数表资料，再用加权法计算，公式如下：

式中：Σflgx为各组频数f与观察值lgx乘积的和。

例7．5 30名麻疹易感儿童接种麻疹疫苗一个月后，血凝抑制抗体滴度如表7－3中第（1）、（2）栏，试求其平均抗体滴度。(www.xing528.com)

表7－3　平均抗体滴度计算表

即30名麻疹易感儿童免疫后的平均血凝抑制抗体滴度为1∶48．5。

（三）中位数与百分位数

1．中位数　将一组变量值从小到大按顺序排列，位置居中的变量值称为中位数（简记为M）。中位数适用于：①变量值中出现个别特小值或特大值；②资料的分布呈明显偏态；③变量值分布一端或两端无确定数值。计算方法有：直接法和频数表法。

（1）直接法：适用于观察值例数较少时。计算前先将观察值按照从小到大的顺序排列，然后使用下面的公式计算。

式中，n为样本的总例数。

例7．6　某医学院校8名临床专业学生的身高（cm）分别是：158、160、160、164、165、166、168、182，求平均身高。

本例中n＝8为偶数，按公式7－7计算：

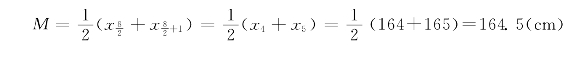
（2）频数表法：适用于观察值例数较多时。首先将观察值编制频数表，再按照公式计算中位数，计算公式为：

式中：LM为中位数所在组段的下限值；i为中位数所在组段的组距；fM为中位数所在组段的频数；n为总例数；ΣfL是小于LM各组段的累计频数。

例7．7 150名食物中毒病人潜伏期分布如表7－4，求其平均潜伏期。

表7－4 150名食物中毒病人潜伏期（小时）的频数分布

从表7－4可以看出，本组数据呈正偏态分布，中位数所在的组段是“12～”，由此可以确定LM＝12，i＝6，fM＝38，n＝150，ΣfL＝64。代入公式7－8得：

即150名食物中毒病人平均潜伏期为13．74小时。

2．百分位数　百分位数是把一组资料的变量值由小到大顺序排列，分为100个等份，与x%相对应的数值即为第x百分位数，记为Px，例如下四分位数、中位数、上四分位数分别记为P25、P50、P75。

计算公式如下：

式中：L、i、fx分别为第x百分位数Px所在组的下限、组距、频数。

例7．8 150名食物中毒病人潜伏期分布如表7－5，求其P25。