非平稳时间序列数据预测：社会统计学成果

上面介绍的平滑法都可以用于描述时间序列的趋势，包括线性趋势和非线性趋势。当用这些方法进行预测时，要注意它们一般只适合平稳时间序列，当序列存在明显的趋势或季节成分时，这些方法就不再适用。 时间序列的趋势可以分为线性趋势和非线性趋势两大类，如果这种趋势能够延续到未来，就可以利用趋势进行外推预测。 有趋势序列的预测方法主要有线性趋势预测、非线性趋势预测和自回归模型，就是前述所介绍的AR（p）模型预测等。

在介绍非平稳序列之前，先给出差分的概念。 用变量xt 的当期值减去其滞后期的数值，从而得到新序列的计算方法称为差分。 若减去的滞后期数是一期，得到的新序列称为原序列的一阶差分；若减数是滞后k 期的数值，得到的新序列称为原序列的k 阶差分。对于一个时间序列数据，如果该序列的特征方程恰好有d 个根在单位圆上，那么，这种时间序列数据就是非平稳的时间序列数据。 这种时间序列的特点是经过d 次差分，可以转化为一个平稳的序列^[1]。

在上述过程中，数据是否平稳对模型的选取及数据的处理至关重要。 那么，如何评估一个时间序列数据是否平稳呢？ 除绘制时间序列数据的走势图之外，更为准确的方法有：时间序列数据的单位根检验、自相关系数和ADF 检验。

例如，美国的GNP 和国内私人总投资INV 是单位为10 亿美元的名义值，价格指数P为GNP 的平减指数（1 972 ＝100），利息率R 为半年期商业票据利息。 回归方程所采用的变量都是实际GNP 和实际投资；它们是通过将名义变量除以价格指数得到的，分别用小写字母gnp，inv 表示。 实际利息率的近似值r 则是通过贴现率R 减去价格指数变化率p得到的。 样本区间：1963—1984 年，建立如下线性回归方程：

回归结果如下：

图11.8　回归结果图

p 阶滞后的Q 统计量的原假设是：序列不存在p 阶自相关；备选假设为：序列存在p阶自相关。

图11.9　残差自相关图

虚线之间的区域是自相关中正负两倍于估计标准差所夹成的。 如果自相关值在这个区域内，则在显著水平为5%的情形下与零没有显著区别。 本例1 阶的自相关系数和偏自相关系数都超出了虚线，说明存在1 阶序列相关。 1 阶滞后的Q 统计量的P 值很小，拒绝原假设，残差序列存在一阶序列相关。

结合我国GDP 变化走势，单位根检验过程，以及通过差分方法化非平稳序列为平稳序列的过程如下。

【例11.5】　表11.7 是我国1978—2004 年的GDP，试建立模型预测2005 年和2006年的GDP 数据。

表11.7　我国1978—2004 年的GDP

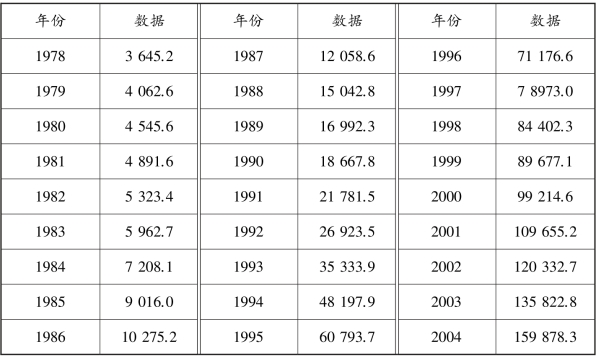
1978—2004 年我国GDP 具有明显的上升趋势。 在ADF 检验时选择含有常数项和时间趋势项，由SIC 准则确定滞后阶数（p ＝4）。 GDP 序列的ADF 检验如下：

图11.10　GDP 序列ADF 检验

检验结果显示，GDP 序列以较大的P 值，即100%的概率接受原假设，即存在单位根的结论。(www.xing528.com)

将GDP 序列做1 阶差分，然后对ΔGDP 进行ADF 检验

图11.11　一阶差分ΔGDP 的ADF 检验

检验结果显示，ΔGDP 序列仍接受存在单位根的结论。 其他检验方法的结果也接受原假设，ΔGDP 序列存在单位根，是非平稳的。

再对ΔGDP 序列做差分，则Δ2GDP 的ADF 检验（选择不含常数项和趋势项）如下：

图11.12　二阶差分ΔGDP 的ADF 检验

检验结果显示，二阶差分序列Δ2GDP 在1%的显著性水平下拒绝原假设，接受不存在单位根的结论，因此可以确定GDP 序列是二阶单整序列。

GDP 序列是二阶单整序列，即GDP ～I （2）。 但是检验得到GDP 的对数序列ln（GDP）是一阶单整序列，所以本例建立Δln（GDP）序列的ARIMA 模型。 首先观察Δln（GDP）序列的相关图。

图11.13　Δln（GDP）序列的相关图

Δln（GDP）序列的自相关系数和偏自相关系数都在一阶截尾，则取模型的阶数p ＝1和q ＝1，建立ARIMA（1，1，1） 模型（时间期间：1978—2004 年，2005 年和2006 年实际数据不参加建模，留作检验）。

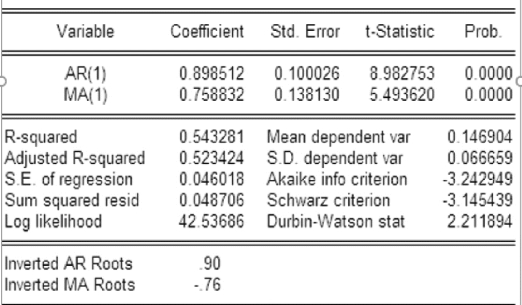
图11.14　ARIMA（1，1，1） 模型回归结果

图11.15　Δln（GDP） 序列的ARIMA（1，1，1）模型残差的相关图

从图11.15 的相关图中可以看出模型的残差不存在序列相关，并且模型的各项统计量也很好。

图11.16 是这个模型的拟合和预测（静态）的结果，其中2005 年和2006 年的预测结果与真实值比较接近，预测效果可以接受。

图11.16　模型的拟合和预测图