社会统计学：平稳序列预测

平稳时间序列，就是没有明显的趋势变化，只是随机地在平均值附近摆动。 时间序列数据的预测模型一般分为4 种类型，即自回归过程、移动平均过程、自回归移动平均过程和单整自回归移动平均过程。 其中前3 种（自回归过程、移动平均过程、自回归移动平均过程）只含有随机波动成分，不含有明显的趋势成分。 因此，平稳序列的预测方法主要有：简单平均法、移动平均法和指数平滑法。

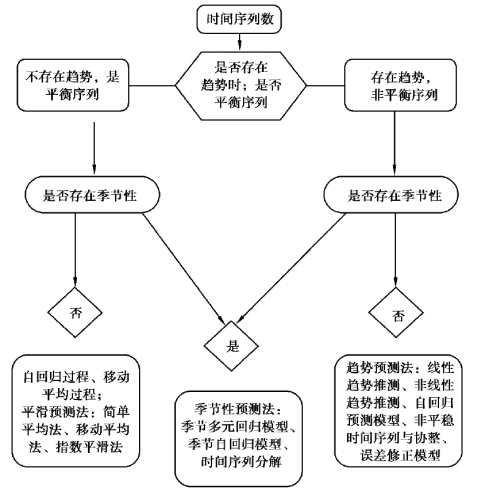
图11.7　时间序列分析流程图

（1）简单平均法

简单平均法，是指用以观察到的t 期数据（Y1，Y2，…，Yt）为依据，预测t＋1 期数据时，直接计算前面已知数据的算术平均值，其计算公式如下：

其中，Ft＋1表示t＋1 期的预测值；Y1，Y2，…，Yt 表示前t 期数据的真实观察值。

（2）移动平均法

移动平均法（moving average），是通过对时间序列逐期递移求得平均数作为预测值的一种预测方法，其方法有简单移动平均法（simple moving average）和加权移动平均法（weighted moving average）两种。

简单移动平均是将最近的k 期数据加以平均，作为下一期的预测值。 比如上证指数5 日均线，就是用5 期数据平均值画出的一条曲线。 类似地，10 日均线、20 日均线、年线等画法原理相同，只是移动间隔不同而已。 以移动间距k ＝5 为例，计算方式如下：设第1期数据到第5 期数据分别为Y1，Y2，…，Y5，则第6 期的预测值为F6：

待第6 期观测值Y6 获得后，则第7 期的预测值为F7 计算如下：

其他预测值以此类推，移动平均法只使用最近k 期的数据，在每次计算移动平均值时，移动的间隔都为k。 该方法也适合对较为平稳的时间序列进行预测。 应用时，关键是确定合理的移动间隔k。

对于同一个时间序列，采用不同的移动间隔，预测的准确性是不同的。 可通过试验选择一个使均方误差最小的移动间隔。

加权移动平均法与上述简单移动平均法类似，只是在计算预测值时，给前k 期数据赋上不同的权重。 有些时间序列数据往往受近期的数据影响比较大，比如，在预测t＋1期数据时，第t 期数据对t＋1 期的数据影响比第t－1 期数据对t＋1 期的数据影响大，因此，在计算移动平均数时，给第t 期数据赋比较大的权重，以此类推。 赋权方法不同，则预测值也不尽相同。

时间序列数据的自回归过程（Auto Regression，或者称作自回归模型）就是一种加权平均法的应用。 如果一个线性随机过程可表示为：

其中，ϕi（i＝1，2，…，p）是回归参数，是前p 期xi（i＝1，2，…，p）的权重；μt 是第t 期随机误差项，是白噪声过程。

此时，称式（11.34）的线性时间序列过程xt 为p 阶自回归过程，用AR（p）来表示。 xt是由p 个滞后项ϕ1xt－1＋ϕ2xt－2＋ϕ3xt－3＋…＋ϕpxt－p和白噪声μt 组成的。

其次，时间序列的移动平均过程也是移动平均的某种表达形式。 如果时间序列过程可以表示成：(www.xing528.com)

其中，θi（i ＝1，2，…，q）是回归参数；μt 是第t 期随机误差项，是白噪声过程，则称式（11.35）为q 阶移动平均过程，记作MA（q）。

若一个随机过程的构造是上述自回归过程和移动平均过程共同组成的，则在对这样的时间序列数据进行预测时，需要建立如下形式的随机过程表达式：

ϕi（i＝1，2，…，p）是回归参数，是前p 期xi（i ＝1，2，…，p）的权重；θi（i ＝1，2，…，q）是回归参数；μt 是第t 期随机误差项；p 和q 分别表示自回归过程和移动平均过程的最大滞后阶数。

满足式（11.36）的过程称为自回归移动平均过程，记作ARMA（p，q）。 这一过程的平稳性只依赖于自回归部分。

在上述3 种时间序列模型中，对于ARMA（p，q）过程和AR（p）过程，如果时间序列数据的特征根都在单位圆内部或单位圆上，则该时间序列就是非平稳的时间序列。 此时，需要采用非平稳时间序列的处理方法。

（3）指数平滑法

指数平滑法（exponential smoothing）是通过对过去的观察值加权平均进行预测的一种方法。 指数平滑法是加权平均的一种特殊形式，观察值的时间越远，其权数呈现指数下降，因而称为指数平滑。 该方法使t＋1 期的预测值等于t 期的实际观察值与t 期的预测值的加权平均值。

指数平滑法有一次指数平滑法、二次指数平滑法、三次指数平滑法等，现在以一次指数平滑法为例介绍指数平滑法。

一次指数平滑法也称单一指数平滑法（single exponential smoothing），它只有一个平滑系数，使得观察值离预测时期越久远，权数变得越小。 一次指数平滑法将一段时期内的预测值与观察值的线性组合作为t＋1 期的预测值，其预测模型为：

式中，Ft＋1表示t＋1 期的预测值；Yt 为t 期的实际观察值；Ft 为t 期的预测值；α 为平滑系数（0＜α＜1）。

由于在开始计算时还没有1 期的预测值F1，通常可以设F1 等于1 期的实际观察值Y1。

2 期的预测值为：

F2 ＝αY1 ＋（1 － α）F1 ＝αY1 ＋（1 － α）Y1 ＝Y1

3 期的预测值为：

F3 ＝αY2 ＋（1 － α）F2 ＝αY2 ＋（1 － α）Y1

4 期的预测值为：

F4 ＝αY3 ＋（1 － α）F3 ＝αY3 ＋α（1 － α）Y2 ＋（1 － α）2Y1

依此类推。