纯随机性检验在社会统计学中的应用

纯随机性检验也称为白噪声检验，是专门用来检验序列是否为纯随机序列的一种方法。 如果一个序列是纯随机序列，那它的序列值之间应该没有任何相关关系，即满足：

这是一种理论上才会出现的理想状态。 实际上，由于观测值序列的有限性，导致纯随机序列的样本自相关系数不会绝对为零。

如果样本自相关图显示这个纯随机序列没有一个样本自相关系数严格等于零，但这些自相关系数确实都非常小，都在零值附近以一个很小的幅度做着随机波动，这时应该考虑样本自相关系数的分布性质，从统计意义上来判断序列的纯随机性质。

式中，n 为序列观察期数。

第一步：假设条件。

原假设：延迟期数小于或等于m 期的序列值之间相互独立。

备择假设：延迟期数小于或等于m 期的序列值之间有相关性。

该假设条件用数学语言描述即为：

H0：ρ1 ＝ρ2 ＝…＝ρm ＝0，∀m≥1；

H1：至少存在某个ρk≠0，∀m≥1，k≤m。

第二步：检验统计量。

①Q 统计量。 为了检验这个联合假设，Box⁃Pierce 推导出了Q 统计量：

式中，n 为序列观察期数，m 为指定延迟期数。(www.xing528.com)

根据正态分布和卡方分布之间的关系，很容易推导出Q 统计量近似服从自由度为m的卡方分布：

②LB 统计量。 在实际应用中人们发现Q 统计量在大样本场合（n 很大的场合）检验效果很好，但在小样本场合就不太精确。 为了弥补这一缺陷，Box 和Ljung 又推导出LB（Ljung⁃Box）统计量：

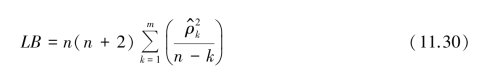
式中，n 为序列观测期数，m 为指定延迟期数。

Box 和Ljung 证明LB 统计量同样近似服从自由度为m 的卡方分布。

实际上LB 统计量就是Box 和Pierce 的Q 统计量的修正，所以人们习惯把它们统称为Q 统计量，分别记作QBP统计量和QLB统计量，在各种检验场合普遍采用的Q 统计量通常指的都是LB 统计量。

【例11.4】　计算表11.5 白噪声序列延迟6 期、延迟12 期的QLB统计量的值，并判断该序列的随机性（α＝0.05）。

表11.5　白噪声随机性判断示例

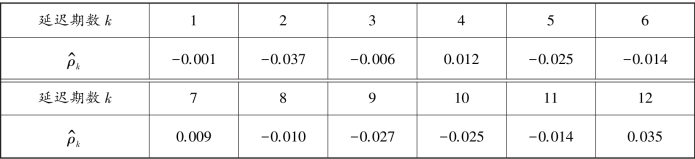
根据上述数据，很容易计算出表11.6 的结果。

表11.6　QLB统计量检验

由于P 值显著大于显著性水平，所以该序列不能拒绝纯随机的原假设。 即可以认为该序列的波动没有任何统计规律可循。

另一方面，假如一个平稳序列显示出显著的短期相关性，那么该序列就一定不是白噪声序列，就可以对序列值之间存在的相关性进行分析。 假如此时考虑的延迟期数太长，反而可能淹没该序列的短期相关性。 因为平稳序列只要延迟期足够长，自相关系数都会收敛于零。