时间序列分析方法作为数理统计学的一个分支,遵循数理统计学的基本原理,都是利用样本信息来推测总体信息。
传统的统计分析通常都拥有如下数据结构,见表11.2。
表11.2 传统统计分析常见数据结构
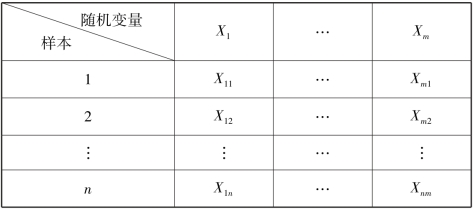
根据数理统计学常识,显然要分析的随机变量越少越好(m 越小越好),而每个变量获得的样本信息越多越好(n 越大越好)。 因为随机变量越少,分析的过程越简单,而样本容量越大,分析的结果就会越可靠。
但是时间序列分析的数据结构有它的特殊性。 对随机序列{…,X1,X2,…,Xt,…}而言,它在任意时刻t 的序列值Xt 都是一个随机变量,而且由于时间的不可重复性,该变量在任意一个时刻只能获得唯一的样本观察值。 因为时间序列分析的数据结构如下,见表11.3。
表11.3 时间序列分析的数据结构

由于样本信息太少,如果没有其他的辅助信息,通常这种数据结构是没有办法进行分析的。 而序列平稳性概念的提出可以有效地解决这个问题。
在平稳序列场合,序列的均值等于常数意味着原本含有可列多个随机变量的均值数列:{ μt,t∈T}变成了一个常数序列{ μ,t∈T}。
原本每个随机变量的均值μt(t∈T)只能依靠唯一的一个样本观察值xt 去估计: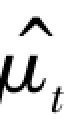 =xt。(https://www.xing528.com)
=xt。(https://www.xing528.com)
现在由于μt =μ(∀t∈T),于是每一个样本观察值xt(∀t∈T),都变成了常数均值μ的样本观察值:

这极大地减少了随机变量的个数,并增加了待估参数的样本容量。 换句话说,这大大降低了时序分析的难度,同时也提高了对均值函数的估计精度。
同理,根据平稳序列二阶矩平稳的性质,可以得到基于全体观察样本计算出来的延迟k 自协方差函数的估计值:
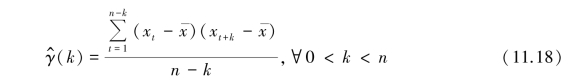
并进一步推导出总体方差的估计值:

和延迟k 自相关系数的估计值:

当延迟阶数k 远远小于样本容量n 时,
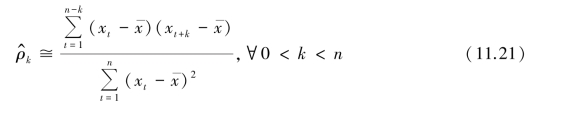
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




