社会统计学中的平稳与非平稳时间序列

平稳时间序列有两种定义，根据限制条件的严格程度，分为严平稳时间序列和宽平稳时间序列。

（1）严平稳

所谓严平稳（strictly stationary）就是一种条件比较苛刻的平稳性定义，它认为只有当序列所有的统计性质不会随时间的推移而发生变化时，该序列才能被认为平稳。 随机变量族的统计性质完全由它们的联合概率分布族决定，所以严平稳时间序列的定义如下：

定义11.1　设｛Xt｝为一时间序列，对任意正整数m，任取t1，t2，…，tm∈T，对任意整数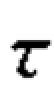，有：

则称时间序列｛Xt｝为严平稳时间序列。

前面说过，在实践中要获得随机序列的联合分布是一件非常困难的事，而且即使知道随机序列的联合分布，计算和应用也非常不便。 所以严平稳时间序列通常只具有理论意义，在实践中用得更多的是条件比较宽松的宽平稳时间序列。

（2）宽平稳

宽平稳（weak stationary）是使用序列的特征统计量来定义的一种平稳性。 它认为序列的统计性质主要由它的低阶矩决定，所以只要保证效率低阶矩平稳（二阶），就能保证序列的主要性质近似稳定。

定义11.2　如果｛Xt｝满足如下3 个条件：

任取t∈T，有＜∞。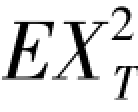

任取t∈T，有EXt ＝μ，μ 为常数。

任取t，s，k∈T，且k＋s－t∈T，有γ（t，s）＝γ（k，k＋s－t）。

则称｛Xt｝为宽平稳时间序列。 宽平稳也称为弱平稳或二阶平稳（second⁃order stationary）。显然，严平稳比宽平稳的条件严格。 严平稳是对序列联合分布的要求，以保证序列所有的统计特征都相同；而宽平稳只要求序列二阶平稳，对于高于二阶的矩没有任何要求。所以通常情况下，严平稳序列也满足宽平稳条件，而宽平稳序列不能反推严平稳成立。

但这不是绝对的，两种情况都有特例。 比如服从柯西分布的严平稳序列就不是宽平稳序列，因为它不存在一、二阶矩，所以无法验证它二阶平稳。 严格地讲，只有存在二阶矩的严平稳序列才能保证它一定也是宽平稳序列。(www.xing528.com)

宽平稳一般推不出严平稳，但当序列服从多元正态分布时，则二阶平稳可以推出严平稳。

定义11.3　时间序列｛Xt｝称为正态时间序列，如果任取正整数n，任取t1，t2.…，tn∈T，相对应的有限维随机变量X1，X2，…，Xn 服从n 维正态分布，密度函数为：

从正态随机序列的密度函数可以看出，它的n 维分布仅由均值向量和协方差阵决定，即对正态随机序列而言，只要二阶矩平稳了，就等于分布平稳了，所以宽平稳的正态序列一定是严平稳时间序列。 对于非正态过程，就没有这个性质了。

在实际应用中，研究最多的是宽平稳随机序列。 以后见到平稳随机序列，如果不加特别注明，指的都是宽平稳随机序列。 如果序列不满足平稳条件，就称为非平稳序列。

（3）非平稳随机过程

尽管以时间序列数据为依据的经验研究都假定有关的时间序列是平稳的，但是也经常会遇到一些非平稳的时间序列。 经典的例子就是随机游走模型（random walk model，RWM），诸如股票价格和汇率之类的资产价格服从随机游走。 随机游走模型可以分为两大类：①带漂移的随机游走（即不存在常数项或截距项），②不带漂移的随机游走（即出现常数项）。

假设μi 是均值为0 和方差为σ2 的白噪音误差项。

把满足式（11.4）的Yt 序列称为随机游走序列。 在如式（11.4）所示的随机游走模型中，Y 在t 时期的值等于其在（t－1）期的值加上一个随机冲击。

如果Y 在t 时期的值与其在（t－1）时期的取值满足式（11.5）的关系，称这一时间序列为带漂移的时间序列。

其中b0 被称为漂移参数（drift parameter）。

将式（11.5）化简整理得：

式（11.6）表明，“漂移”的含义是指Yt 根据b0 为正或负而向上或向下漂移。