如何识别和处理多重共线性问题，社会统计学成果

检测多重共线性的方法有许多种，其中最简单的方法就是计算各自变量之间的相关系数。 如果相关系数数值的绝对值仅为1，则表明各自变量之间很可能存在多重共线性问题。 除此之外，如果出现以下情况，则表明自变量之间存在多重共线性的可能性很大。

具体来说，如果有以下情形出现，则暗示存在多重共线性的可能性很大：

第一种情形：构建的多元回归模型中各自变量之间显著相关。

第二种情形：当多元回归模型的总体线性关系检验（F 检验）显著时；同时，几乎所有回归系数的t 检验却不显著。 这种情形暗示存在多重共线性。

第三种情形：回归系数的正负号与预期的相反。 特别是，回归系数的正负号与已有经济学理论预期的正负号相反，则此时要注意多重共线性问题。

第四种情形：方差膨胀因子越大，多重共线性越严重。 一般认为VIF 大于10 时，认为存在严重的多重共线性。(www.xing528.com)

多重共线性问题带来的主要麻烦是对单个回归系数的解释和检验。 因此，在建立多元线性回归模型时，不要试图引入更多的自变量，除非确实有必要。

如果在回归估计的过程中，发现模型中存在多重共线性问题，就应采取某种方法来解决多重共线性问题。 解决多重共线性的一般方法有：

第一种方法：将一个或多个相关的自变量从模型中剔除，使保留的自变量尽可能不相关。

第二种方法：在多元回归模型中如果出现多重共线性问题，同时又想要在模型中保留所有的自变量，此时需要：①避免对单个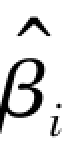参数进行t 检验；②在对因变量y 进行推断预测时，应该将y 值尽可能地限定在自变量样本值的范围内。