【摘要】：对于多重判定系数R2，有一点需要注意： R2 是出现在模型中的自变量个数的非减函数，即随着自变量个数的增加，R2 几乎必然增大而不会减小。当增加自变量时，会使预测误差变得较小，从而减少残差平方和SSE。由于回归平方和SSR ＝SST－SSE，当SSE 变小时，SSR ＝SST－SSE 就会变大，从而使R2 变大。因此，在比较两个模型的拟合优度时，贸然地选择高的R2 就必须当心。因此，在多元回归分析中，通常用调整的多重判定系数。
对于多重判定系数R2，有一点需要注意： R2 是出现在模型中的自变量个数的非减函数，即随着自变量个数的增加，R2 几乎必然增大而不会减小。 这将影响因变量的变差中被估计的回归方程所解释的比例。 当增加自变量时，会使预测误差变得较小，从而减少残差平方和SSE。 由于回归平方和SSR ＝SST－SSE，当SSE 变小时，SSR ＝SST－SSE 就会变大，从而使R2 变大。 如果模型中增加一个自变量，即使这个自变量在统计上并不显著，R2 也会变大。
因此，在比较两个模型的拟合优度时，贸然地选择高的R2 就必须当心。 在比较两个模型的R2 时，必须要考虑模型中出现的自变量的个数。 为避免增加自变量而高估R2，统计学家提出用样本量n 和自变量的个数k 去调整R2，计算出调整的多重判定系数（adjusted multiple coefficient of determination），记为
，其计算公式为：(www.xing528.com)
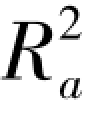的解释与R2 类似，不同的是： 
同时考虑了样本量n 和模型中自变量的个数k的影响，这就使得
的值永远小于R2，而且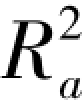
的值不会由于模型中自变量个数的增加而越来越接近1。 因此，在多元回归分析中，通常用调整的多重判定系数。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
