社会统计学：确定性与非确定性关系剖析

确定性关系是指当一些变量的值确定以后另一些变量的值也随之完全确定的关系，这些变量间的关系完全是已知的，可以用函数y ＝f（x1，x2，…，xi）来表示。 如圆的面积S与半径r 之间的关系S ＝πr2；电路中电阻值R、电压U 与电流I 之间的关系U＝IR 等。

类似于一元回归方程中，因变量与自变量之间的非确定性关系，多元回归方程中因变量与自变量之间的关系也是非确定性的对应关系。 非确定性关系是指变量之间有一定的依赖关系，但当一些变量的值确定以后，另一些变量值虽然随之变化，却不能完全确定，这时变量间的关系就不可以精确地用函数来表示。 这类非确定的关系大量存在。 如人的体重W 与身高H 有密切的关系但是这种关系不能用函数关系来表达；又如，某种乔木的树干高度H 与树干的直径D 有密切的关系但是这种关系也不能用函数关系来表达。再如孩子的身高Y 与父亲的身高X1 及母亲的身高X2 之间有一定的关系，但是这种关系同样不能用函数关系来表达；人的脚掌的长度X 与身高Y 也有类似的相关关系。 这些例子中变量间的关系是不确定关系（即相关关系）。

在上面的几个例子中，人的身高H、树干的直径D、父亲的身高X1 及母亲的身高X2都可看成能够根据研究需要在一定的范围内随意地取指定的值的非随机变量，相当于函数关系中的自变量，称为预报变量（也称可控变量）；而人的体重W、树干的高度H、孩子的身高H 则都是随机变量，它们的值虽然可以观察但是不能预先确定，称为相应变量（也称可控变量），它们相当于函数关系中的因变量。

回归分析是数理统计中研究一个相应变量与若干个预报变量之间相关关系的一种有效方法，利用估计结果做预测和控制，回归分析在金融保险事业及各个领域都有着广泛的应用。 在大量重复试验中，由不确定性的变量所呈现出的统计规律性，称为统计相关。 两个变量之间的相关关系称为单相关，3 个以上变量的相关关系称为复相关，把在复相关条件下仅研究两个变量间的相关关系称为偏相关。

【案例】(www.xing528.com)

销售额与流通费率、广告投放的关系

某百货公司为了了解百货商店销售额x 与流通费率y（流通费率，是反映商业活动的一个质量指标，指每一元商品流转额所分摊的流通费用）之间的关系。 其收集到两者之间的数据关系（销售额从小到大排列）如下：

表10.1　店铺销售额与流通费率、广告费用数据

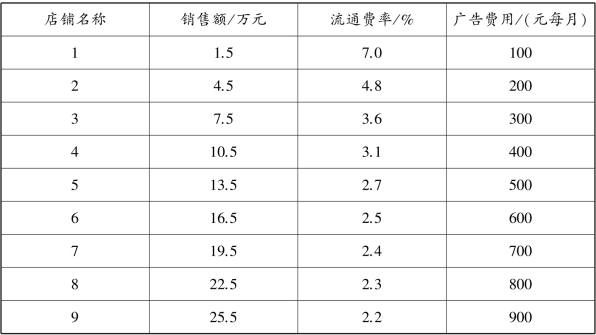
那么，这两者之间是否存某种对应关系呢？ 他们之间的对应关系是否明显？ 这就需要对这些数据对进行相互关系的验证。 下面是对数据对进行相关性描述的方法介绍。