双因素方差分析在社会统计学中的交互作用

在每一种水平配合（Ai，Bj）下重复做m（m≥2）次试验，称为有交互作用的双因素试验，试验结果观测数据xijk列于下表：

表9.9　有交互作用的双因素试验观测数据结构

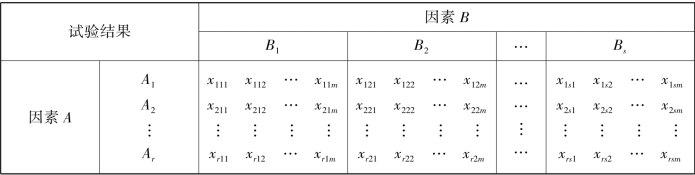
并设在水平配合（Ai，Bj）下的数据xij1，xij2，…，xijm来自总体Xij ～N（μij，σ2）（i ＝1，2，…，r；j＝1，2，…，s）。

检验如下假设：

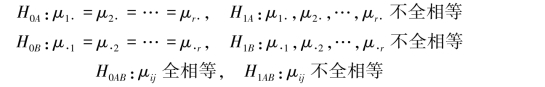
分别用如下检验统计量：

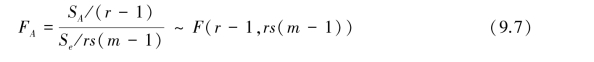
对于给定的显著性水平α（α ＝0.01 或0.05），如果FA ＞Fα（r－1，rs（m－1）），则拒绝H0A，即认为因素A 对试验指标有显著影响；如果FB＞Fα（s－1，rs（m－1）），则拒绝H0B，即认为因素B 对试验指标有显著影响；如果FAB＞Fα（（r－1）（s－1），rs（m－1）），则拒绝H0AB，即认为因素A 与因素B 之间的交互效应对试验指标有显著影响。

实际计算时，可事先对原始数据作如下处理：

这时再进行计算，不会影响FA，FB，FAB值的大小。

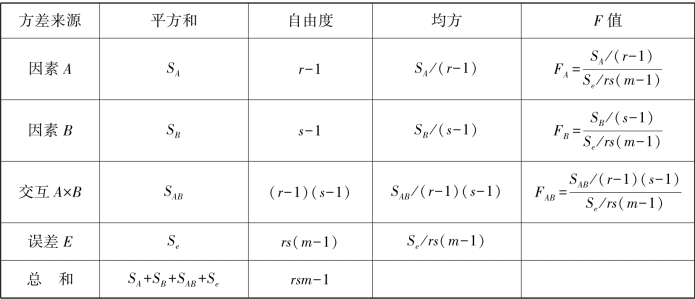
结果列于下面的方差分析表9.10。(www.xing528.com)

表9.10　有交互作用的双因素方差分析表

【例9.3】　考察合成纤维弹性影响因素为拉伸倍数A 与收缩率B。 A 与B 各取4 个水平，每个水平配合下做两次试验，结果数据见表9.11。

表9.11　合成纤维弹性影响因素数据表

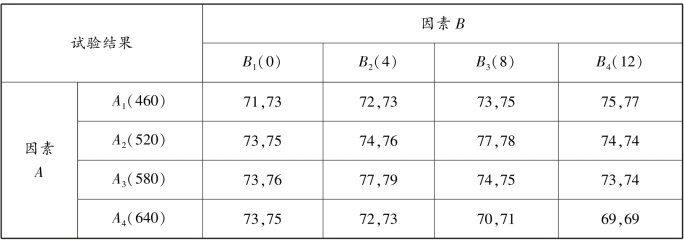
试分析因素A、因素B 对合成纤维弹性的影响是否显著？ 以及因素A 与因素B 之间的交互效应对合成纤维弹性的影响是否显著？

解　r＝4，s＝4，m＝2

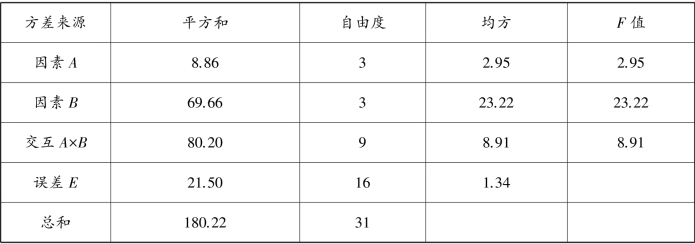
SA ＝8.86，SB ＝69.66，SAB ＝80.20，Se ＝21.50

FA ＝2.95＜F0.05（3，16）＝3.24，说明拉伸倍数A 对合成纤维弹性无显著影响。

FB ＝23.22＞F0.01（3，16）＝5.29，说明收缩率B 对合成纤维弹性的影响高度显著。

FAB ＝8.91＞F0.01（9，16）＝3.78，说明因素A 与因素B 之间的交互效应对合成纤维弹性的影响高度显著。

表9.12　合成纤维弹性影响因素方差分析表