区间估计与假设检验在社会统计学中的关系

考虑显著性水平为α 的双边检验，

由显著性水平为α 的假设检验的拒绝域的定义，检验（8.19）的拒绝域为：

另一方面，对于∀θ0∈Θ ，考虑显著性水平为α 的假设检验问题，

H0：θ ＝θ0，H1：θ ≠θ0

由θ0 的任意性，即对∀θ∈Θ ，有：

由此说来，为求参数θ 的置信水平为1－α 的置信区间，先求出显著性水平为α 的假设检验问题：H0：θ＝θ0，H1：θ≠θ0 的接受域：

综上所述，假设检验的接受域是区间估计的置信区间，故假设检验与区间估计的统计处理是相通的。 假设检验和参数估计（区间）都是统计问题。 在总体已知，参数未知的情况下总体的一些性质可归结为参数的性质。 假设检验与参数估计是从不同方面回答同一问题。 如纺纱厂纺出的纱的强力是否达标，通过样本观察值的研究，假设检验的回答是“是或否”，参数估计回答的是强力是多少（或范围）。 即假设检验所讨论的问题是否成立，回答是定性的，而参数估计则从“量”的方面给出回答。

【例8.11】　设X～N（μ，1），μ 未知，α＝0.05，n ＝16，且由一个样本值计算得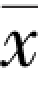 ＝5.20。根据前面的条件，对总体均值的置信区间与假设检验求解。

解　①由区间估计结果进行假设检验。(www.xing528.com)

根据题目条件，得到参数μ 的一个置信水平为1－α 的置信区间为：

根据区间估计结果，可以进行双侧检验。 于是

考虑检验问题：H0：μ＝5.2，H1：μ≠5.2，

因为样本均值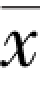 ＝5.2∈（4.71，5.69），故接受H0。

②由假设检验结果给出相应的区间估计。

因此，右边检验问题的接受域为μ0＞4.79。

这样就得到μ 的单侧置信区间（4.79，∞），单侧置信下限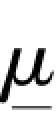＝4.79。