社会统计学：评价估计量的标准

参数估计是用样本估计量θ≫作为总体参数θ 的估计。 实际上，用于估计θ 的估计量有很多，比如，可以用样本均值作为总体均值的估计量，也可以用样本中位数作为总体均值的估计量，等等。 那么，究竟用样本的哪种估计量作为总体参数的估计呢？ 自然要用估计效果最好的那种估计量。 什么样的估计量才算是一个好的估计量呢？ 这就需要有一个公认的评价标准。 统计学家给出了评价估计量的一些标准，主要有以下几个。

（1）无偏性

估计量是一个随机变量，对于不同的样本会得到不同的估计值。 那么进行参数估计的时候，都希望估计值越接近真实值越好。 然而真正估计值等于真实值往往是难以达到的，因此，希望估计统计量能够很好地去估计未知参数，即希望估计值不要偏高也不要偏低。 由此，对估计量引入了无偏性的判定标准。

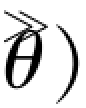无偏性（unbiasedness）是指估计量抽样分布的数学期望等于被估计的总体参数。 设总体参数为θ，所选择的估计量为，如果E（＝θ，则称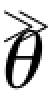为θ 的无偏估计量。

（2）有效性

(www.xing528.com)

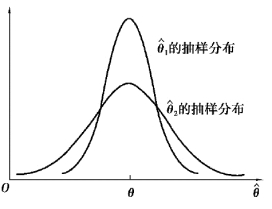
图7.3　两个无偏估计量的抽样分布

（3）一致性（相合性）

一致性（consistency）是指随着样本量的增大，估计量的值越来越接近被估总体的参数。 换言之，一个大样本给出的估计量要比一个小样本给出的估计量更接近总体的参数。 根据样本均值的抽样分布可知，样本均值抽样分布的标准差为，由于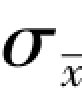与样本量大小有关，样本量越大，的值就越小。 因此可以说，大样本量给出的估计量更接近总体均值μ。 从这个意义上说，样本均值是总体均值的一个一致估计量。