非线性回归的应用及意义

【案例】

非线性关系的应用

下图是历年广交会的客商来自国家和地区的数量与成交额的相关散点图。

从图中可以看出，广交会客商来自国家和地区的数量与广交会成交额之间并不呈线性关系，而是呈非线性关系，因此无法用直线来拟合两个变量之间的关系。 这时，就需要用到非线性回归。

（1）非线性回归方程的建立

如果变量x 与y 之间不是简单的线性关系，则用线性回归方程来拟合就不能很好地反映变量之间的关系，用线性回归方程进行预测也得不到很好的预测结果。 从图5.4 中可以看出，x 与y 之间并不是线性关系，而是非线性关系。 这时如果再用直线来拟合就不能很好地说明两个变量之间的关系了，会产生很大的误差。

图5.4　x 与y 的散点图

在这种情况下，可以用曲线来拟合x 与y 之间的关系，这种方法称为非线性回归。 与线性回归方程的建立一样，也可以采用最小二乘法来建立非线性回归方程。 如果用二次曲线来拟合变量之间的关系，非线性回归方程为：

设Q 为总误差平方和，则有：

分别求Q 对a，b，c 的偏导数得：

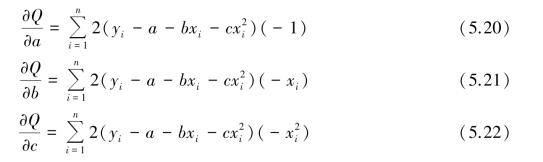
令上述3 个导数等于0，得到关于a，b，c 的三元一次方程组：

(www.xing528.com)

求解上述三元一次方程组可得：

由于求解a，b，c 的过程涉及大量数据高次方的运算，因此计算非常麻烦。 如果拟合三次曲线或其他复杂的曲线，则计算量更大，这使得非线性回归方程的应用受到了限制。但是，计算机统计分析解决了大量数据计算繁杂的问题，用统计软件进行非线性回归分析的操作也很简单。 目前，非线性回归也得到了有效的应用。

（2）非线性回归分析的应用

非线性回归首先要根据散点图中的数据分布来选择拟合函数。 如果数据分布呈现明显的曲线特征，则选择一个形状与其相近的曲线方程，求解出相应的系数，即可建立非线性回归模型。 在统计软件SPSS 中给出的下面10 种曲线方程，可作为拟合函数：

①Linear：直线。 与一元回归分析完全相同，拟合的数学模型为：y ＝a＋bx。

②Quadratic：二次曲线。 拟合的数学模型为：y ＝a＋bx＋cx2。

③Compound：复合函数曲线。 拟合的数学模型为：y ＝a＋bx。

④Growth：等比级数曲线。 拟合的数学模型为：y ＝ea＋bx。

⑤Logarithmic：对数曲线。 拟合的数学模型为：y ＝a＋b ln x。

⑥Cubic：三次曲线。 拟合的数学模型为：y ＝a＋bx＋cx2＋dx3。

⑦S：S 形曲线。 拟合的数学模型为：y ＝。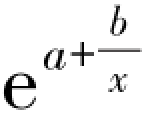

⑧Expoential：指数函数曲线。 拟合的数学模型为：y ＝a＋ebx。

⑨Inverse：反比例函数曲线。 拟合的数学模型为：y ＝a＋。

⑩Power：幂函数曲线。 拟合的数学模型为：y ＝a＋xb。

非线性回归与线性回归的不同点在于，对于一组观察值可以拟合多种曲线，计算的工作可以交给计算机来完成。 研究者根据判定系数R2 的大小，可以从中选择拟合优度最好的曲线。