通过散点图可以判断两个变量之间有无相关关系,并对变量间的关系形态作出大致的描述,但散点图不能准确反映变量之间的关系强度。 因此,为准确度量两个变量之间的关系强度,需要计算相关系数。 对于非线性的相关关系,由于比较复杂,因此从略,这里仅介绍线性的相关关系。 线性相关关系的强度是通过线性相关系数来度量的,简称相关系数r。
(1)协方差
图5.2 表示了变量x 和变量y 之间存在相关关系的散点图,它共有n 对数据:
(x1,y1)
(x2,y2)
︙
(xn,yn)
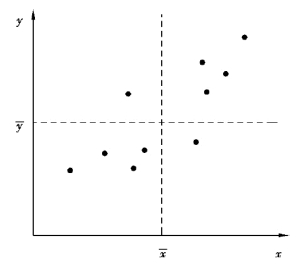
图5.2 x 和y 的散点图
x 和y 的均值为:
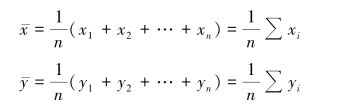
把坐标轴移到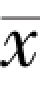 和
和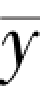 ,于是对于新的坐标,其观测值为:
,于是对于新的坐标,其观测值为:
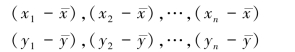
现在来研究x 和y 每对数据的乘积:
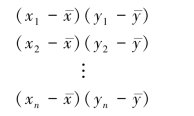
显然,如果观测值落在新坐标的第一或第三象限,则乘积
![]()
反之,如果观测值落在新坐标的第二或第四象限,则乘积
![]()
可以想象,如果变量x 和y 之间存在线性相关关系的话,则其观测点不会平均地分散在四个象限,而只会集中在一三象限或二四象限。 线性相关程度愈强,其集中的程度愈明显。 从数量上来考虑,则上述乘积的总和可以作为线性相关程度的标志。

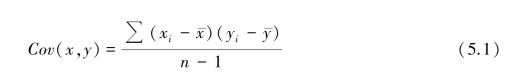
实际上,协方差的概念是不难理解的。 变量的方差公式为:
![]()
它表示变量观测值相对其均值的平均偏差,因此协方差则表示变量x 和y 的观测值相对其各自均值所造成的共同平均偏差。
(2)相关系数r
协方差的数量可以作为变量线性相关程度的度量,但由于它的数值与单位有关,因此不同单位的变量还无法进行比较。 为此,将变量标准化,然后再求其乘积的平均。
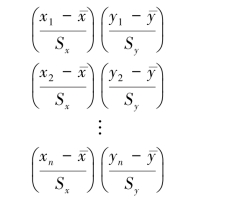
取平均有:
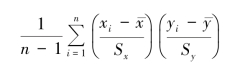
这就是样本数据的相关系数r。 对于总体数据而言,相关系数r 为:(https://www.xing528.com)
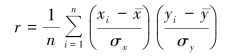
但无论是样本数据还是总体数据,相关系数r 都可写作:
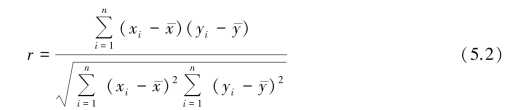
可见,相关系数就是标准化了的协方差。 数值上,它等于协方差除以各自标准差的乘积。 相关系数,正如协方差一样,都是度量变量间的线性相关程度的。
将式(5.2)整理后可以得到一个相关系数常用的导出公式:
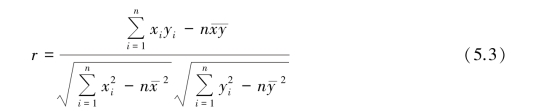
用式(5.3)计算相关系数r 比用式(5.2)相对简单一些。
为解释相关系数各数值的含义,需要对相关系数的性质有所了解。 相关系数的性质可总结如下:
第一,相关系数r 的取值范围为[-1,1],即-1≤r≤1。 若0<r≤1,表明x 和y 之间存在正线性相关关系;若-1≤r<0,表明x 和y 之间存在负线性相关关系;若r =1,表明x 和y 之间为完全正线性相关关系;若r=-1,表明x 和y 之间为完全负线性相关关系;当r =0时,y 的取值与x 无关,二者之间不存在线性相关关系。
第二,相关系数r 具有对称性。 x 与y 之间的相关系数rxy和y 与x 之间的相关系数ryx相等,即rxy =ryx。
第三,相关系数r 仅仅是x 与y 之间线性关系的一个度量,它不能用于描述非线性关系。 这意味着,r=0 只表示两个变量之间不存在线性相关关系,并不说明变量之间没有任何关系,它们之间可能存在非线性相关关系。 变量之间的非线性相关程度较大时,可能会导致r=0。 因此,当r=0 或很小时,不能轻易得出两个变量之间不存在相关关系的结论,而应结合散点图作出合理的解释。
第四,相关系数r 虽然是两个变量之间线性关系的一个度量,却不意味着x 与y 一定有因果关系。

【例5.1】 请计算表4.13 中这10 名学生语文成绩和数学成绩的相关系数r。
表5.2 10 名学生的语文成绩和数学成绩统计表
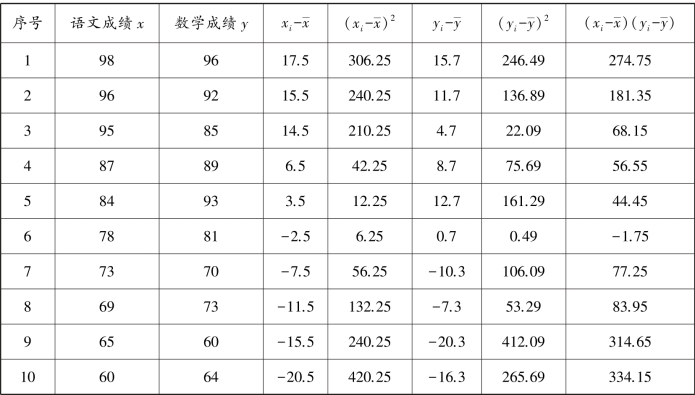
解 根据表4.13 中10 名学生的语文成绩和数学成绩可得:

根据式(5.2)得:
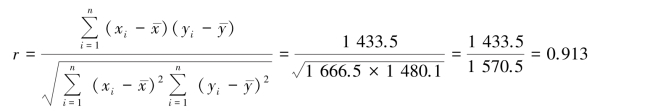
计算结果表明,这10 名学生的语文成绩和数学成绩间有很强的正相关关系,相关系数为0.913。
【例5.2】 表5.3 列出了10 个家庭的月收入与住房面积数据,请计算月收入与住房面积的相关系数r。
表5.3 月收入与住房面积统计表
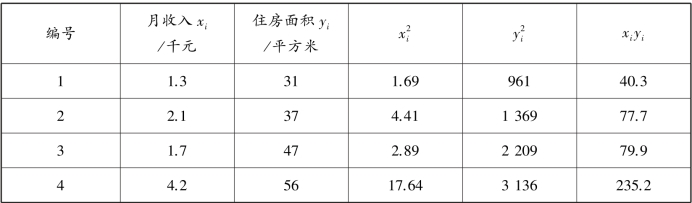
续表
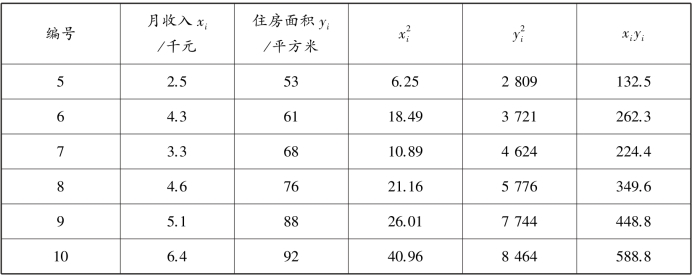

根据式(5.3)得:

计算结果表明,这10 个家庭的月收入和住房面积间有很强的正相关关系,相关系数为0.921。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




