社会统计学：肯德尔系数探究

在Gamma 等级相关系数的计算中，只考虑了同序对和异序对的作用，而没有考虑同分对的作用，这在同分对非常多的情况下会使计算出的相关系数偏大。 因此，统计学家肯德尔（Kendall）对此进行了修正。

肯德尔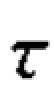相关系数的分子仍然是同序对数ns 和异序对数nd 的差，只是分母作了修正。 采用不同的修正方法，可构建不同的等级相关系数。 肯德尔将等级相关系数分以下3 种情况来讨论。

（1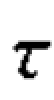）a

a 系数仍以同序对数ns 与异序对数nd 之差作为分子，但以样本容量n 所形成的总对数为分母，因此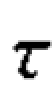a 的计算公式为：

显见，当数据中全是同序对时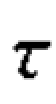，a ＝1；反之，当数据中全是异序对时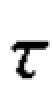，a ＝－1。 因此，a 的取值范围为［－1，1］。

（2）b

当出现同分对时，肯德尔将分母作了如下的修正：

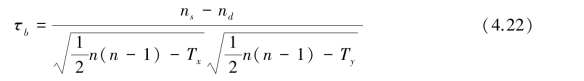
其中，Tx 表示变量x 方向的全部同分对数，Ty 表示变量y 方向的全部同分对数。 当出现x和y 方向都同分时，在两个方向都要计算进去。 同时，当某个等级i 出现不止1 个同分对时，还要计算两两同分对所形成的数据对。 因此，Tx 和Ty 有如下的计算：

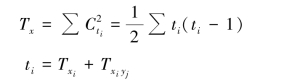
ti 包括在i 等级上，仅x 同分的对数Txi和x、y 都同分的对数Txi yj之和。(www.xing528.com)

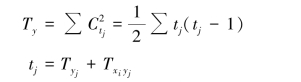
tj 包括在j 等级上，仅y 同分的对数Tyj和x、y 都同分的对数Txi yj之和。

（3）c

当同分对很多的情况下，肯德尔先将数据做成等级的列联表。 对于由两个定序变量构成的r×c 的列联表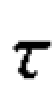，c 的计算公式为：

其中，m＝min（r，c），即m 为r×c 等级列联表中r 和c 值中的较小者。

【例4.9】　请计算表4.17 中父辈文化程度和子辈文化程度的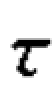c 等级相关系数。

解　由例4.8 可知，ns ＝55 842，nd ＝6 833。

表4.17 是一个3×3 交叉列表，因此m＝min（3，3）＝3，代入式（4.21）可得：

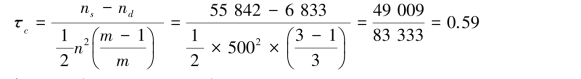
结算结果表明，父辈文化程度和子辈文化程度呈现出较强的正相关关系。

对比例4.8 和例4.9 可知，利用同一组数据计算出的Gamma 等级相关系数的绝对值要大于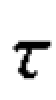c 系数。