Gamma等级相关系数在社会统计学中的应用

【案例】

Gamma 等级相关系数的应用

下表是882 名不同文化程度的城市居民对周围环境满意度的调查结果。

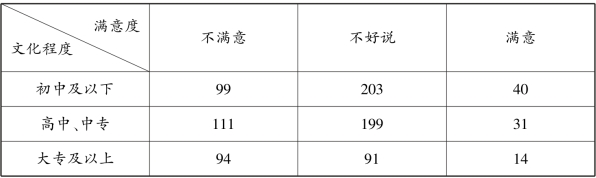
当要求计算文化程度与环境满意度的等级相关系数时，由于斯皮尔曼等级相关系数主要适用于小样本中的变量以及取值很多的尺度变量之间关系的计算，显然其在本例中并不适用。 这时，就可以选择Gamma 等级相关系数。

由于斯皮尔曼等级相关系数仅适用于变量没有相同等级或只有少量的相同等级，但在社会调查中的定序变量大多仅有几个取值，而样本数往往成百上千，这必然导致大量的数据处于相同等级。 这时，斯皮尔曼等级相关系数就不能有效地测量定序变量间的等级相关。 在这种情况下，可以用Gamma 等级相关系数来描述两个定序变量之间的相关程度，其不受样本容量的限制。 Gamma 等级相关系数是用同序对与异序对的数量差来测量两个变量的相关程度的。

（1）同序对、异序对和同分对

1）同序对

设单元A 变量x 和y 具有等级（xi，yi），单元B 变量x 和y 具有等级（xj，yj），若当xi＞xj 时，yi＞yj，则称A 和B 是同序对。 可见，同序对只要求x 变化方向与y 变化方向相同，但并不要求A 与B 中x 的变化量xi－xj 与y 的变化量yi－yj 相等。

2）异序对

设单元A 变量x 和y 具有等级（xi，yi），单元B 变量x 和y 具有等级（xj，yj），若当xi＞xj 时，yi＜yj，则称A 和B 是异序对。 可见，异序对只要求x 变化方向与y 变化方向相反，但并不要求A 与B 中x 的变化量｜xi－xj ｜与y 的变化量｜yi－yj ｜相等。

3）同分对

设单元A 变量x 和y 具有等级（xi，yi），单元B 变量x 和y 具有等级（xj，yj），若变量x具有相同的等级，即xi ＝xj，则称为x 同分对；若变量y 具有相同的等级，即yi ＝yj，则称为y同分对；若变量x 与变量y 等级都相同，即xi ＝xj 且yi ＝yj，则称为x、y 的同分对。

例如，在表4.14 中，序号为1 与2、1 与3、2 与4、3 与6 等个体均为同序对；序号为2与5、7 与8 等个体均为异序对；序号为3 与4、4 与5、8 与9、9 与10 等个体均为同分对。

【例4.7】　请以表4.15 中的单元数据，列举其中的同序对、异序对和同分对。

表4.15　单元数据

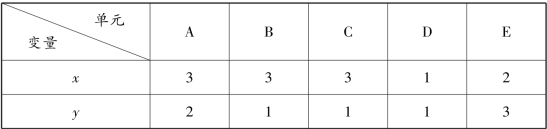
解　单元对数共有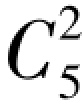 ＝10，先以A 为基础来讨论。

AB：x 同分对

AC：x 同分对

AD：同序对

AE：异序对

再依次以B，C，D 为基础来讨论

BC：x，y 同分对

BD：y 同分对(www.xing528.com)

BE：异序对

CD：y 同分对

CE：异序对

DE：同序对

在列联表中存在大量的同序对和异序对。 现以3×3 交叉列表为例，说明同序对和异序对的计算方法，其他结构的列联表也可以参考使用。 设列联表4.16 中两个定序变量x和y 的取值情况为x3＞x2＞x1 且y3＞y2＞y1。

表4.16　3×3 列联表

n11，n12和n13的个体在变量x 上取值相同，均为x1，属于同分对；n11，n21和n31的个体在变量y 上取值相同，均为y1，也属于同分对。 可见，在列联表中同一行或同一列的个体均构成同分对。

n22，n32，n23和n33的个体在变量x 和y 上的取值都大于n11对应的取值，因此，它们与n11的个体可以构成同序对。 同理，n21与n32，n33的个体构成同序对，n12与n23，n33的个体构成同序对，n22与n33的个体也构成同序对。

设ns 为同序对数目，则3×3 列联表中同序对数为：

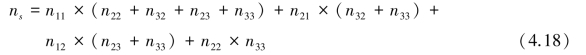
n21，n22，n31和n32的个体在变量x 上的取值都大于n13，而在变量y 上的取值都小于n13，因此，它们与n13的个体构成异序对。 同理，n12的个体可以与n21，n31的个体构成异序对，n23的个体可以与n31，n32的个体构成异序对，n22的个体可以与n31的个体构成异序对。

设nd 为异序对数目，则3×3 列联表中异序对数为：

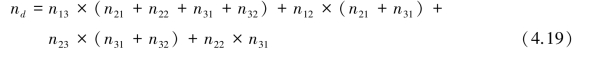
（2）Gamma 等级相关系数的计算

明确了同序对和异序对的概念后可以看出，在两个变量的分布中，如果同序对多而异序对少，则表明两个变量之间存在正相关关系；反之，如果异序对多而同序对少，则表明两个变量之间存在负相关关系。 按照这种思想构建的Gamma 等级相关系数的计算公式为：

其中，ns 为同序对的数目，nd 为异序对的数目。

当两个变量完全正相关时，nd ＝0，G ＝1；当两个变量完全负相关时，ns ＝0，G ＝－1。 可见，G 的取值范围为［－1，1］。 Gamma 等级相关系数不仅表明了两个定序变量相关程度的大小，而且表明了相关的方向。

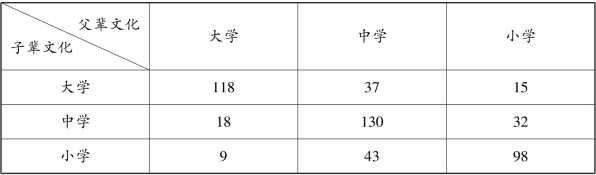
【例4.8】　表4.17 是500 名被调查者文化程度代际流动的抽样调查结果，请计算父辈文化程度和子辈文化程度的Gamma 等级相关系数。

表4.17　文化程度代际流动的抽样调查结果

解　由Gamma 等级相关系数的计算公式可知：

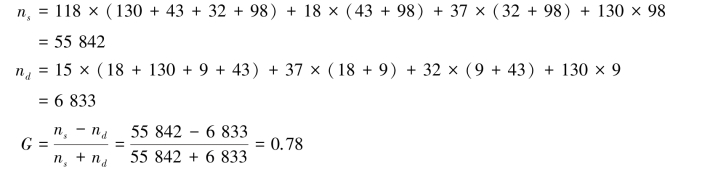
可见，父辈文化程度与子辈文化程度之间呈现较强的正相关关系。