(1)构建斯皮尔曼等级相关系数的统计思想
斯皮尔曼等级相关系数是根据每个个体在两个变量上的等级差值来测量两个变量的相关程度的。 将两个变量对应的两组数据分别排序后,每个个体在两个变量上分别获得了一个等级。 如果两个变量有比较强的正相关关系,个体的两个等级差就会比较小,所有个体的两个等级差值的平方和也会比较小;反之,如果两个变量有比较强的负相关关系,个体的两个等级差就会比较大,所有个体的两个等级差值的平方和也会比较大。 因此,所有个体的两个等级差值的平方和可以用来测量两个变量的等级相关程度。
(2)斯皮尔曼等级相关系数的计算
先举一例予以说明,假设调查了5 对夫妻,他们双方的家庭社会经济地位如表4.12所示。
表4.12 夫妻双方家庭社会经济地位统计结果
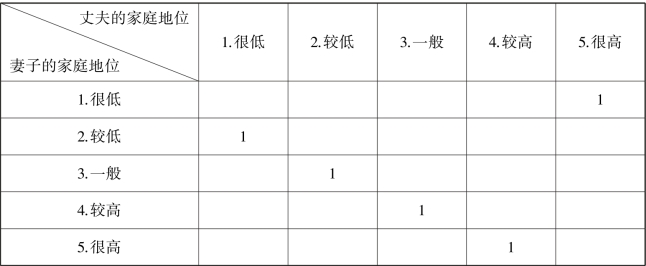
我们把一对夫妻称作上述配对样本中的一个单元,于是这5 对夫妻可写作5 个单元:
(1,2)
(2,3)
(3,4)
(4,5)
(5,1)
现在来计算每一对夫妻家庭社会经济地位的等级差的平方:
(1 - 2)2
(2 - 3)2
(3 - 4)2
(4 - 5)2
(5 - 1)2
可以想象,等级差的平方和极小值为0,它表示双方家庭都是严格按照高配高、低配低,这称作完全的正等级相关:
(1 - 1)2
(2 - 2)2
(3 - 3)2
(4 - 4)2
(5 - 5)2
相反,如果双方家庭严格按照高配低、低配高,则称作完全的负等级相关,这时等级差的平方和为极大值:
(1 - 5)2
(2 - 4)2
(3 - 3)2
(4 - 2)2
(5 - 1)2
斯皮尔曼等级相关系数就是以上述等级差的平方和为基础来讨论等级相关的。 设样本共有n 对单元,其中x 共有n 个等级,y 也有n 个等级。
x 等级:1,2,3,…,n
y 等级:1,2,3,…,n
设每一个单元x 和y 的观察值为:
(x1,y1)
(x2,y2)
︙
(xn,yn)
它们等级差的平方为:(https://www.xing528.com)
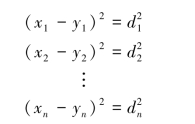
斯皮尔曼等级相关系数rs 的计算公式为:

其中,di 为第i 个个体在两个变量上的等级差;n 为个体总数,也是等级总数。
当x 和y 完全正等级相关时,有:
x1 =y1
x2 =y2
︙
xn =yn
因此:
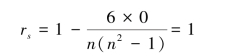
当x 和y 完全负等级相关时,有:

因此有:
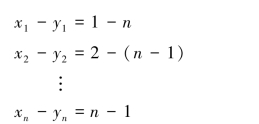
此时,x 和y 等级差的平方和 将达到极大值(∑
将达到极大值(∑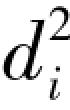 )max。
)max。
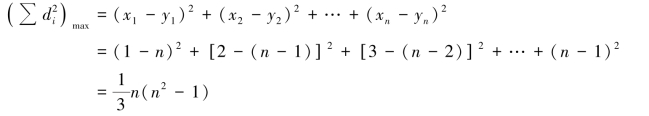
代入式(4.17),得:
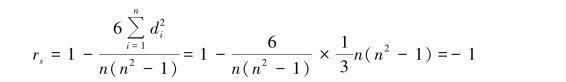
可见,当两个变量完全正相关时,rs =1;当两个变量完全负相关时,rs =-1。 即rs 的取值范围为[-1,1]。
1)无相同等级的斯皮尔曼等级相关系数的计算
设变量x 与y 均为定序变量,且不含相同等级。 也就是说,在任何一个变量上都不存在两个个体取值相同的情况,每个个体占有一个等级。 此时,可以直接利用式(4.17)计算斯皮尔曼等级相关系数。
【例4.5】 表4.13 列出了10 名学生的语文成绩和数学成绩,请计算这10 名学生语文成绩和数学成绩的斯皮尔曼等级相关系数。
表4.13 学生的语文成绩和数学成绩统计表(一)
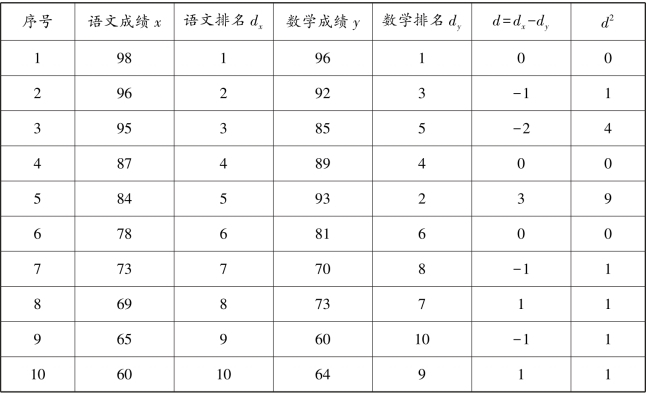
解 由斯皮尔曼等级相关系数的计算公式可得
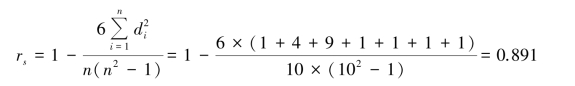
可见,这10 名学生语文成绩和数学成绩的正等级相关程度很高。
2)有相同等级的斯皮尔曼等级相关系数的计算
如果在一个变量中两个个体的取值相等,就会出现相同等级。 在统计学中,相同等级也称为“结”。 对于结的处理一般是采用具有相同等级的个体所应占有的平均等级作为它们的共同等级,这样就能保证个体数与等级数基本一致。 当相同等级不太多时,也可以计算斯皮尔曼等级相关系数。
【例4.6】 表4.14 列出了10 名学生的语文成绩和数学成绩,其中成绩排名含有相同等级,请计算这10 名学生语文成绩和数学成绩的斯皮尔曼等级相关系数。
表4.14 学生的语文成绩和数学成绩统计表(二)
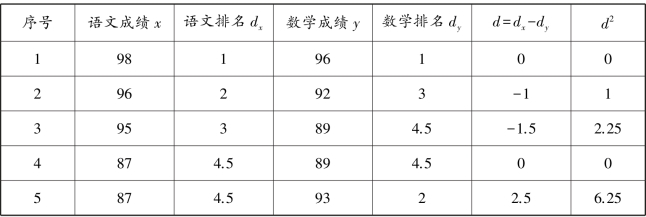
续表
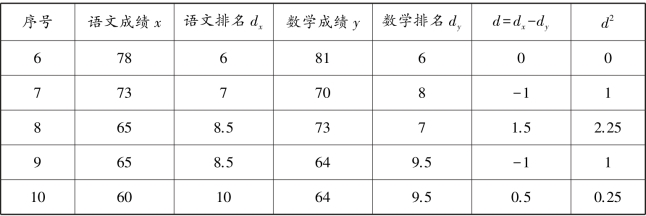
解 这10 名学生在语文成绩排名和数学成绩排名上的处理见表4.14,由斯皮尔曼等级相关系数的计算公式可得

可见,这10 名学生语文成绩和数学成绩的正等级相关程度很高。
由于斯皮尔曼等级相关系数要求没有相同等级,因此当变量的取值不是很多但个体数很多时,这个要求是难以满足的。 以年龄为例,年龄的取值只有100 多个,如果调查的个体有10 000 人,则必然会有很多同龄的人,这些同龄人自然会有相同的等级。 从这个角度看,斯皮尔曼等级相关系数主要适用于小样本中的变量以及取值很多的尺度变量之间关系的计算。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




