社会统计学：如何计算年龄段与电视节目类型的相关系数

系数也是基于消减误差比例的思想构建的列联相关系数，但是对E1 和E2 的定义与λ 系数中的有所不同。 仍以表4.10 中学生是否愿意参加课外辅导为例，说明系数计算中E1 和E2 的定义方法。

在不知道变量x 和y 相关的情况下，猜测每个个体的y 值时，只能参考y 的边缘分布。为了更多地利用变量y 边缘分布的信息，不再用众数对y 进行猜测，而是改用y 边缘分布的比例进行猜测。 具体做法是，将表4.10 中的200 人随机地分为110 人和90 人两组。 将110人这一组的个体都猜测为愿意参加课外辅导，对于这组学生的态度猜错的人数为：

将90 人这一组的个体都猜测为不愿意参加课外辅导，对于这组学生的态度猜错的人数为：

这样猜测产生的误差E1 为：

当知道变量x 和y 相关后，将100 名男生随机分为40 人和60 人两组。 将40 人这一组的个体都猜测为愿意参加课外辅导，而将60 人这一组的个体都猜测为不愿意参加课外辅导。 那么，对于男生的态度猜错的人数为：

同理，将100 名女生随机分为70 人和30 人两组。 将70 人这一组的个体都猜测为愿意参加课外辅导，而将30 人这一组的个体都猜测为不愿意参加课外辅导。 那么，对于女生的态度猜错的人数为：

这样，猜测产生的误差E2 为：

消减误差比例为：

依据上述方法计算出的PRE 即为系数。 下面以列联表4.2 为例，讨论系数的一般形式。

将式（4.11）和式（4.12）代入式（4.5），得：

当变量x 和y 不相关时，边缘频率分布等于条件频率分布：(www.xing528.com)

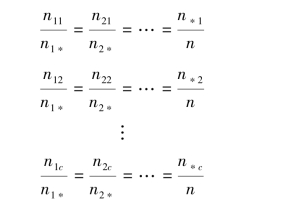
因此，下列各式可用边缘分布来表示：

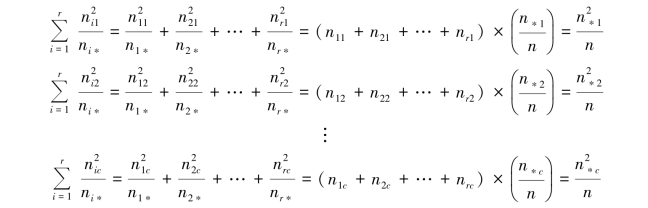
把以上c 个式子加总起来，则有：

将式（4.14）代入式（4.13），由于分子为0，所以有：

当变量x 和y 完全相关时，表4.2 中的各列及各行均只有一个不为0 的频次，因此边缘分布的值与各列的nij值相等，则：

将式（4.15）代入式（4.13），分子与分母相等，因此：

可见，当变量x 和y 不相关时，y ＝0；当变量x 和y 完全相关时，y ＝1。

与λ 系数一样，如果借助y 来猜测x，定义的E1 和E2 是不同的，计算出的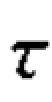系数也是不同的，即系数也具有不对称性。

借助y 来猜测x 的系数的计算公式为：

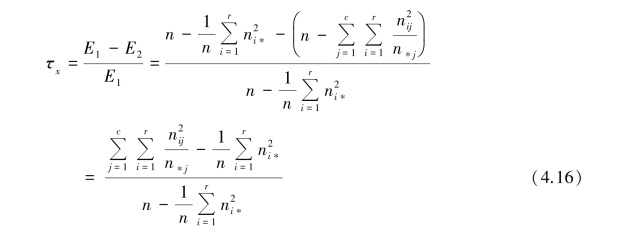
【例4.4】　请计算表4.1 中年龄段与电视节目类型间的系数。

解　设节目类型为变量x，年龄段为变量y，则：

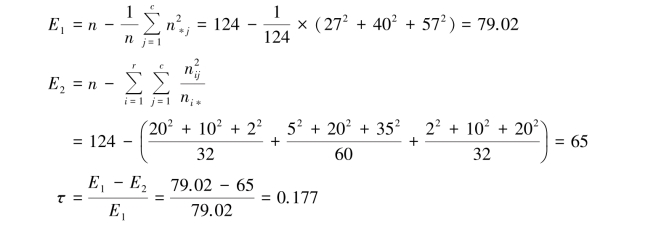
即年龄段与电视节目类型的系数为0.177。

与λ 系数相比，系数中E1 和E2 的定义稍显复杂，但系数比较充分地利用了样本数据的信息。 因此，一般认为，表明变量之间相关程度的系数比λ 系数更为准确。